Wie bestimme ich Extremstellen des Kosinus´ ohne eine Ableitung zu benutzen?

Question

Hallo !

ich soll zu der Funktion f(x)=1-2cos(2x-(π/3)) die Extremstellen bestimmen, ohne dabei eine Ableitung zu benutzten ..

Kann mir bitte jemand sagen, wie das gehen soll ? :/

!:))

Answer 1

Hi, man könnte die Gleichung \(f(x)=1\) lösen. Genau die Mitten von je zwei benachbarten Lösungen dieser Gleichung sind die Extremstellen von \(f\). Nun muss man nur noch begründen, warum das so ist.

Answer 2

Der Extremwert des cos () liegt bei 0, π, -π, 2 * π, 2 * -π,usw

Die Extremwerte von 1 - 2 * cos ()  dürften auch bei
0, π, -π, usw liegen

f(x)=1-2cos(2x-(π/3))

also Extremwert
2cos(2x-(π/3))   = 2 * cos (0 )
2 * x - π / 3 = 0
2 * x = π / 3
x = 2 / 3 * π

Über die erste Ableitung
f ´( x ) = 2 * -sin ( 2 * x - π / 3 ) * 2
2 * -sin ( 2 * x - π / 3 ) * 2 = 0
4 * -sin ( 2 * x - π / 3 )  = 0
-sin ( 2 * x - π / 3 ) = 0
2 * x - π / 3 = 0
x = 2 / 3 * π  dasselbe wie oben

Die andern Extremstellen wären auch noch zu bestimmen
Hier noch der Graph


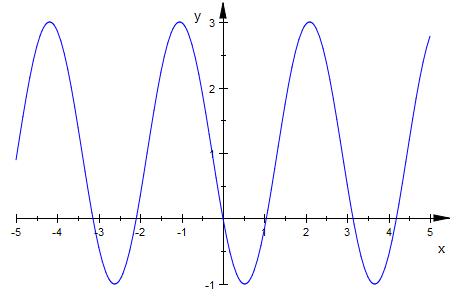
Alle Angaben ohne Gewähr.