Exponentialfunktion: Zeitpunkt, an dem die Zahl der Echsen die Zahl 1000 unterschreitet?

Question

Aufgabe Exponentialfunktion:

In Südamerika ist eine bestimmte Echsenart vom Aussterben bedroht. Die Population (in Tausend) hat sich in den vergangenen Jahren nach nebenstehendem Verlauf entwickelt. Der starke Rückgang bis zum Zeitpunkt kann durch die Funktion \( f(x)=-0,22 x^{2}+5,4 \) dargestellt werden. Ab dem Zeitpunkt 3 kann der Rückgang abgeschwächt werden. Diese Phase ist durch die Funktion \( g(x)=10 \cdot 0,7^{x} \) beschrieben werden.

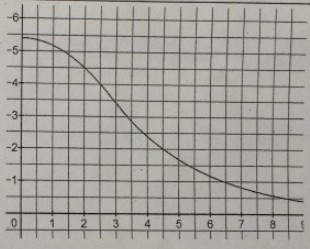
a) Berechnen Sie die Anzahl der Tiere zum Zeitpunkt 3.

b) Berechnen Sie den genauen Zeitpunkt, an dem die Zahl der Tiere die Zahl 1000 unterschreitet.

c) Wie viele Tiere gibt es noch zum Zeitpunkt 10?

d) Wann wäre die Tierart ausgestorben, wenn sich der Prozess zwischen dem Zeitpunkt 0 und dem Zeitpunkt 3 so weiter fortgesetzt hätte?

Answer 1

rechne doch, wann es genau 1000 ist

10 * 0,7^x = 1
0,7^x = 0,1

x* ln(o,7) = ln(o,1)

x =  ln(o,1) / ln (o,7)   =  6,45

Also nach etwa 6,5 Jahren.   Zeigt die Grafik auch.

Answer 2

g(x) = 10 * 0.7^x = 1 --> x = LN(1/10)/LN(0.7) = 6.456

Das stimmt mit der Skizze überein.

Comments

aber ich versteh nicht wieso man da = 1 schreibt anstatt 1000

---

Lies den Text aufmerksam. Die Population (IN TAUSEND) ...

Answer 3

Hier meine Berechnungen

aber ich versteh nicht wieso man da = 1 schreibt anstatt 1000

Wie im Begleittext angeführt gelten die Funktionen für
y = 1 entspricht 1000 Echsen