Bestimmung einer Wahrscheinlichkeitsdichtefunktion aus gegebenen Messdaten

Question

Ich habe für mein Abitur ein Matheprojekt zu machen. Aufgabenstellungen:

Projektarbeit zur Stochastik

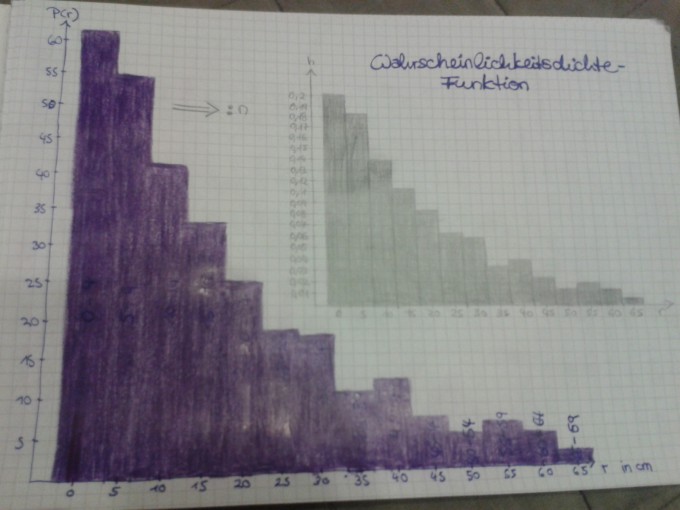
Bei einem Spiel werden Münzen gegen eine Wand geworfen und der Abstand der Münze zur Wand gemessen, wenn die Münze liegen bleibt. Gewinner ist, wessen Münze am nächsten an der Wand liegt. Die gemessenen Abstände einer Spielserie finden Sie in der Tabelle unten.

a) Bestimmen Sie die Wahrscheinlichkeit dafir, dass der Abstand der Münze zur Wand kleiner \( 20 \mathrm{~cm} \) ist.

b) Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Münze in einem Abstand von \( 10 \mathrm{~cm} \) bis \( 20 \mathrm{~cm} \) liegen bleibt.

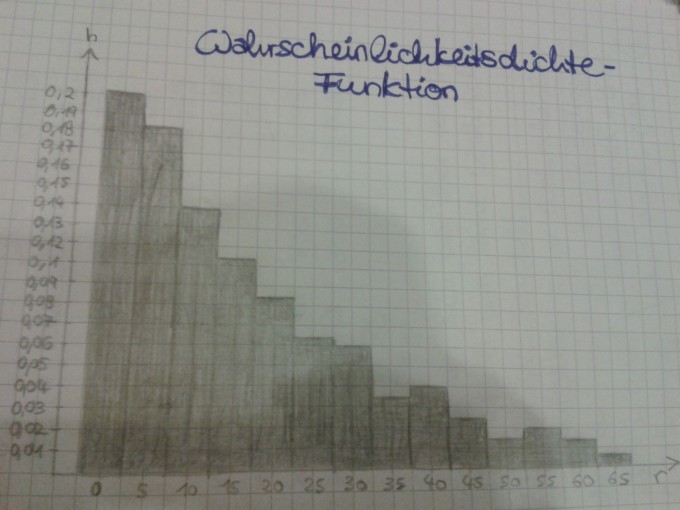
c) Stellen Sie eine zu den Daten passende Wahrscheinlichkeitsdichtefunktion auf.

Tipp: Es ist einfacher, wenn Sie als Maßeinheit \( [d m] \) benutzen, prinzipiell können Sie aber jede Längeneinheit nutzen.

d) Beweisen Sie, dass es sich bei der von Ihnen gefundenen Funktion um eine Wahrscheinlichkeitsdichtefunktion handelt.

e) Diskutieren Sie, wie gut Ihre Wahrscheinlichkeitsdichtefunktion zu den gegebenen Daten passt.

Ansatz/Problem:

a) und b): Hier wäre ich euch dankbar, wenn ihr einfach über meine Rechnung drüber guckt und mich auf eventuell Fehler hinweist.

c): Ich bin mir nicht sicher ob das Erstellen eines Histogramms als Aufstellen einer Wahrscheinlichkeitsdichtefunktion reicht oder ob ich hier eine Funktion im Sinne f(x)=? herausfinden muss. Wenn ja, wie? Durch eine Exponentialfunktion annähern? Wenn ja, wie sehe dann die Rechnung (analytisch) aus? Oder die Funktion stückweise definieren? Da sie ja nicht konstant fällt?

d): Die Kriterien einer Wahrscheinlichkeitsdichtefunktion sind doch  x= >0 und die Fläche unter der Funktion = 1. ?! Beide Kriterien sind erfüllt. Ist damit bewiesen, dass es sich um eine Wahrscheinlichkeitsdichtefunktion handelt? Oder wie muss ich hier weiter argumentieren?

e): An dieser scheitere ich. Dafür brauche ich doch nun wirklich eine Funktion im Sinne f(x)=? oder? Und wieso sollte meine Funktion nicht zu den Daten passen, sie ist doch daraus entstanden? Oder ist damit wirklich eine näherungsweise Funktion gemeint?

Answer 1

Du hast die Aufgabe ja schonmal gestellt. Also (a) und (b) scheinen mit ok. Bei (c) und (d) habe ich eine andere Ansicht. Die berechneten relativen Häufigkeiten sind wohl richtig, ohne das ich die Zahlenwerte im Detail kontrolliert habe, aber der Ansatz ist ok. Allerdings muss meiner Meinung nach nicht die Summe der relativen Häufigkeiten  \( 1 \) ergeben, sondern das Integral über der Dichtefunktion. Und da Du als Klassenhöhe die relative Häufigkeit genommen hast, muss diese noch mit der Intervallbreite multipliziert werden und über alle Klassen summiert werden, und das ergibt nicht \( 1 \). Das ergibt sich nur, wenn die relativen Häufigkeiten noch durch die Intervallbreiten dividiert werden.

Soweit dazu.

Nun zu Teil (e)

Eine Möglichkeit ist, die diskrete Dichtefunktion durch eine stetige Dichtefunktion zu approximieren und die Korrelation dieser stetigen Dichtefunktion mit den gegebenen Daten zu berechnen. Ist dieser Korrelationskoeffizient nahe bei \( 1 \) ist eine gute Korrelation gegeben, sonst nicht.

Nun entnehme ich dem Verlauf der Häufigkeitsverteilung, dass man diese durch eine Exponentialfunktion der Form \( f(x;\alpha,\beta) = \alpha e^{\beta x}\) approximieren kann. Die Parameter \( \alpha \) und \( \beta \) sind dabei so zu bestimmen, dass der Ausdruck
$$ (1) \quad \sum_{i=1}^{N} \left[ f(x_i;\alpha,\beta) - y_i \right]^2 $$ minimal wird. Dabei sind \( x_i \) die Klassenmitten und \( y_i \) die Klassenhöhen. Im besten Fall gilt also $$ (2) \quad  y_i = f(x_i;\alpha,\beta) $$ dann wird der Ausdruck \( (1) \)identisch \( 0 \)

Um das Problem einfacher zu gestalten wird (2) logarithmiert und es ergibt sich
$$ (3) \quad ln(y_i) = ln(\alpha) + \beta x_i  $$ Um \( (1) \) zu lösen, muss also der Ausdruck
$$ F(\alpha,\beta) = \sum_{i=1}^{N}\left[ ln(y_i) - ln(\alpha) - \beta x_i \right]^2 $$ in Abhängigkeit von \( \alpha \) und \( \beta \) minimiert werden, wemm man eine quadratische Optimierung möchte.

Dazu muss gelten
$$ (4) \quad \frac{\partial F}{\partial \alpha} = 2 \cdot \sum_{i=1}^{N} \left[ ln(y_i) - ln(\alpha) - \beta x_i \right] \cdot \left( -\frac{1}{\alpha} \right) = 0 $$ und
$$ (4) \quad \frac{\partial F}{\partial \beta} = 2 \cdot \sum_{i=1}^{N} \left[ ln(y_i) - ln(\alpha) - \beta x_i \right] \cdot \left( -x_i \right) = 0 $$
Also muss folgendes Gleichungssystem gelöst werden
$$ \begin{pmatrix}  N & \sum_{i=1}^{N} x_i \\ \sum_{i=1}^{N} x_i & \sum_{i=1}^{N}x_i^2 \end{pmatrix} \begin{pmatrix} ln(\alpha) \\ \beta \end{pmatrix} = \begin{pmatrix} \sum_{i=1}^{N}ln(y_i) \\ \sum_{i=1}^{N} ln(y_i \cdot x_i) \end{pmatrix}  $$
Es ergibt sich also
$$ \begin{pmatrix} ln(\alpha) \\ \beta \end{pmatrix} = \frac{1}{N \cdot \sum_{i=1}^{N}x_i^2 -\left( \sum_{i=1}^{N}x_i \right)^2} \begin{pmatrix}  \sum_{i=1}^{N}x_i^2 \cdot \sum_{i=1}^{N}ln(y_i) - \sum_{i=1}^{N}x_i \cdot \sum_{i=1}^{N}ln(y_i) x_i \\ N \cdot \sum_{i=1}^{N} ln(y_i) x_i - \sum_{i=1}^{N} x_i \cdot \sum_{i=1}^{N} ln(y_i)  \end{pmatrix}  $$

Damit sind die Parameter \( \alpha \) und \( \beta \) bestimmt.

Mit diesen Parametern ist aber dir Funktion \( f(x;\alpha,\beta) \) noch keine Dichte, da ja gelten muss

$$  \int_0^\infty f(x;\alpha,\beta) dx = 1 $$ Daraus ergibt sich also eine Exponentialverteilung.

Der Korrelationskoeffizient nach https://de.wikipedia.org/wiki/Korrelationskoeffizient ergibt einen Wert von \(  0.979 \), also eine hohe Übereinstimmung der gefundenen Dichtefunktion mit den Daten.

Comments

"... , muss diese noch mit der Intervallbreite multipliziert werden und über alle Klassen summiert werden, und das ergibt nicht 1. Das ergibt sich nur, wenn die relativen Häufigkeiten noch durch die Intervallbreiten dividiert werden."

Hä? Das hebt sich doch auf?

---

"Der Korrelationskoeffizient nach https://de.wikipedia.org/wiki/Korrelationskoeffizient ergibt einen Wert von 0.979, also eine hohe Übereinstimmung der gefundenen Dichtefunktion mit den Daten."

Das habe ich nicht verstanden. Wie berechnet man die Korrelation von einer Distribution mit einem Datensatz?

Answer 2

Für c) kannst Du diese Formel angeben:

\(H(x,\sigma)=\frac{1}{N}\sum_{n=1}^{N}\mathcal{N}(x-D(n),\sigma) \)

Das ist vermutlich nicht was der Aufgabensteller im Sinn hatte aber immer eine korrekte Antwort.

Wie so oft ist die Aufgabenstellung schlecht formuliert. Was der Aufgabensteller eigentlich meint ist vermutlich:

c) Wählen Sie aufgrund eines Histogramms eine passende Verteilungsfunktion aus und bestimmen sie deren Parameter.

Wie Du richtig erkannt hast passt die Exponentialverteilung.

d) Müsste lauten: Zeigen Sie, dass die von Ihnen bestimmte Funktion den Ansprüchen an eine Stetige Wahrscheinlichkeitsverteilung gerecht wird.

e) Am besten Du zeigst, dass die kumulierte Verteilungsfunktion mit der kumulierten Anzahl der Messpunkte korreliert.

\( \int\limits_{0}^{\infty}f(x) \propto \frac{1}{N} \vert \{ n ∈ D \vert (D ≥ x) \}\vert\)

D ist Dein Datensatz und \( N = \vert D \vert\)