Beschreiben Sie wesentliche Eigenschaften der Funktionenschar: fk(x):=(x^2 - k)/(x^2+k) -x, x∈R, k∈R.
Die nachfolgende Zeichnung zeigt einige Graphen dieser Schar:
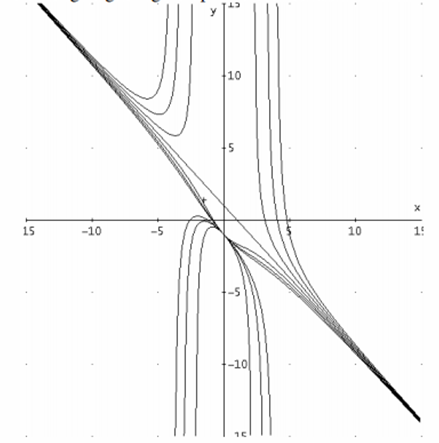
a) Beschreiben Sie wesentliche Eigenschaften, Unterschiede und Gemeinsamkeiten der Graphen.
b) Untersuchen Sie, welche Graphen sich im Punkt P(0/-1) schneiden.
c) Zeigen Sie: Es gibt genau einen Graphen, der einen Sattelpunkt hat.
d) Untersuchen Sie, für welche Parameter die Graphen Polstellen besitzen.
e) Der Graph von fk (k>0) schließt mit dem Graphen von f0 eine Fläche ein. Berechnen Sie den Flächeninhalt dieser Fläche.
f) Ak sei der Flächeninhalt der Fläche, die der Graph von fk (k>0) mit den Koordinatenachsen im dritten Quadranten einschließt.
f1) Berechnen Sie (näherungsweise) A0,5. f
f2) Begründen Sie, dass für die Flächen gilt: Ak 0,5.