Berechne die Turmhöhe. + Berechne den Winkel α, den die Raumdiagonale eines Würfels mat einer Kante bildet.

Question

Aufgabe 14:

a) Eine Turmspitze erscheint von einer Stelle aus, die in horizontaler Richtung 141 m vom Fuß des Turms entfernt ist unter einem Erhebungswinkel von 48,5°. Berechne die Turmhöhe, wenn die Augenhöhe 1,50 m beträgt.

b) Versucht in ähnlicher Weise die Höhe eines Kirchturms in eurer Umgebung zu bestimmen. Überlegt, wie stark sich die Messfehler auf das Ergebnis auswirken können.

Aufgabe 21:

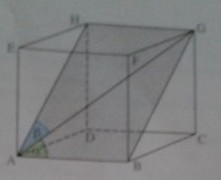
a) Berechne den Winkel α, den die Raumdiagonale eines Würfels mat einer Kante bildet.

b) Welchen Winkel β bildet die Raumdiagonale mit einer Seitenfläche?

Aufgabe 22:

Ein Quader hat die Kante a = 5 cm; b = 4 cm; c = 3 cm. Berechne die Winkel α, β, γ, welche die Raumdiagonale des Quaders mit den Kanten a, b, c bildet.

Answer 1

Nr. 14 a)

Turmhöhe (ohne Augenhöhe) = tan(48.5°)*141m  =159,37 m

→Der Turm ist 159.37m + 1,5m= 160,87 m hoch.

Nr. 21

Der Würfel habe die Katenlänge a. Zu berechnen ist der Winkel α im Dreieck ABG. Man berechnet zuerst die Länge der Strecke BG, also der Flächendiagonalen:

BG= √(2a²) = √2a

tan(α) = (√2a)/a = √2

α=54,7 °

tan(β) = a/(√2a)= 2^-0,5

β= 35,3°

Nr.22

Skizze:

BD= √((4cm)²+(3cm)^2) = 5cm

tan(α)= 5/5=1

α=45°

AC= √((5cm)^2) +(3cm)^2) = √(34cm^2) =5,83 cm

tan(β) = 5,83/4

β= 55,55

BF= √((5cm)^2)+(4cm)^2)= √(41cm^2)= 6,4 cm

tan(γ)= 6,4/3

γ=64,9°