Berechne die Winkel Alpha, Beta, Gama, welche die Raumdiagonale mit den Kanten a, b, c des Quaders bildet.

Question

Aufgabe:

Bei einem Quader ist die Kante b halb so lang wie die Kante a und die Kante c halb so lang wie b. Berechne die Winkel Alpha, Beta, Gama, welche die Raumdiagonale mit den Kanten a, b, c des Quaders bildet.

Problem/Ansatz:

Hallo, ich habe leider keinen Ansatz, wie ich die Aufgabe lösen muss. Ich habe bisher nur eine Planfigur gezeichnet.

Comments

Der Winkel α ist falsch eingezeichnet.

Answer 1

Wenn c=1 ist, ist b=2 und a=4.

Es ist d=√(a^2+b^2+c^2)=√(21).

Betrachte das rechtwinklige Dreieck BCH.

Der Winkel β zwischen d und b befindet sich bei B.

cosβ=b/d=2/√(21) --> β

Die anderen Winkel entsprechend.

☺

Comments

Vielen Dank!!!!

Answer 2

Du hast jeweils drei Seitenlängen (bzw. kannst sie leicht herausfinden). Und dann würde ich den Cosinussatz verwenden.

Comments

Und wie finde ich meine Seitenlänge heraus?

---

Die Seitenlänge von den Dreiecken, nicht Deine... Mit dem Satz des Pythagoras.

Answer 3

Hallo,
meine eigene Skizze ist leider etwas krumm geraten.

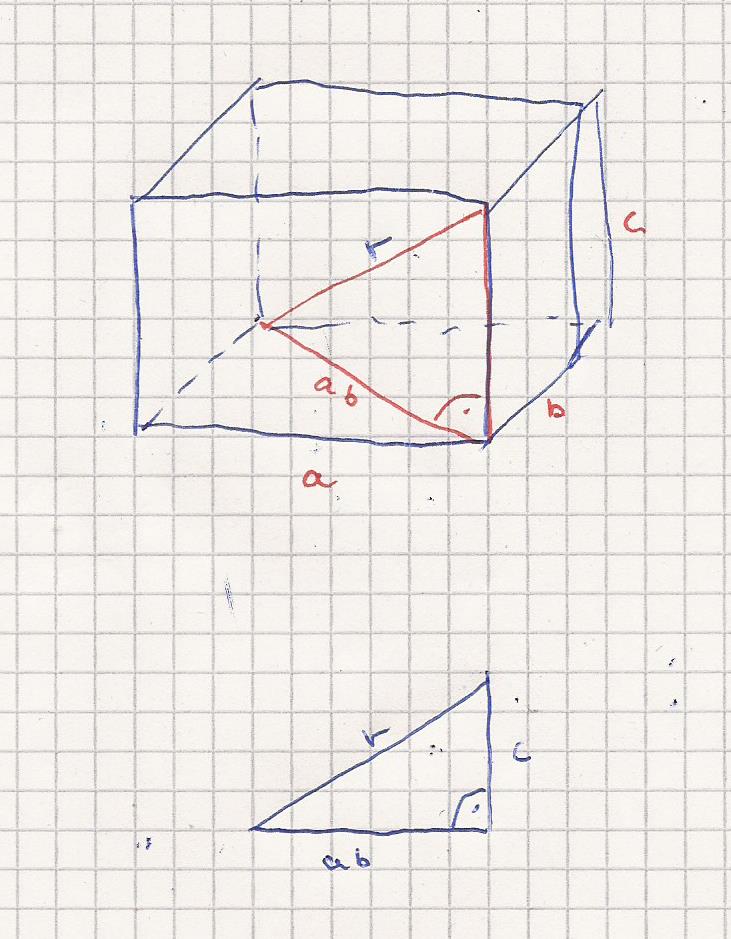
Kanten
a
b = a/2
c = b/2 oder a/4

Die Flächendiagonale ab ( Pythagoras ) ist
ab^2 = a^2 + b^2 = a^2 + ( a/2)^2 = 5/4 a^2
ab = a * √ (5/4)

Es gilt nun den Winkel in der unteren hinteren Ecke
zwischen ab und c zu bestimmen.
ab, c, und r ist ein rechtwinkliges Dreieck,
tan ( alpha ) = c / ab
tan ( alpha ) = ( a/4 ) / (a * √ (5/4))
tan ( alpha ) = ( 1/4 ) / √ (5/4)
tan ( alpha ) = 0.2236
alpha = 12.6 °

Bitte alles nachprüfen.

Bei Fragen wieder melden.

mfg Georg