Berechnen Sie die Stammfunktion. Bestimmen Sie die abgesetzte Stückzahl bis zur 50. Woche. (Porzellanhersteller)

Question

Aufgabe:

Ein Porzellanhersteller legt anlässlich der Hochzeit des schwedischen Prinzen Carl Philip mit Sofia Hellquist im Sommer 2015 eine Sammeltasse auf. Aus Erfahrung mit ähnlichen Ereignissen geht man davon aus, dass sich der Absatz gemäß der Funktion \( f(t)=\left(t^{2}+2 t\right) \cdot e^{-0,2 t+1} \) ergibt. Dabei gibt \( t \) die Zeit in Wochen an und \( f(t) \) den wöchentlichen Absatz in ME je Woche. Nach 50 Wochen wird der Posten aus dem Programm genommen.

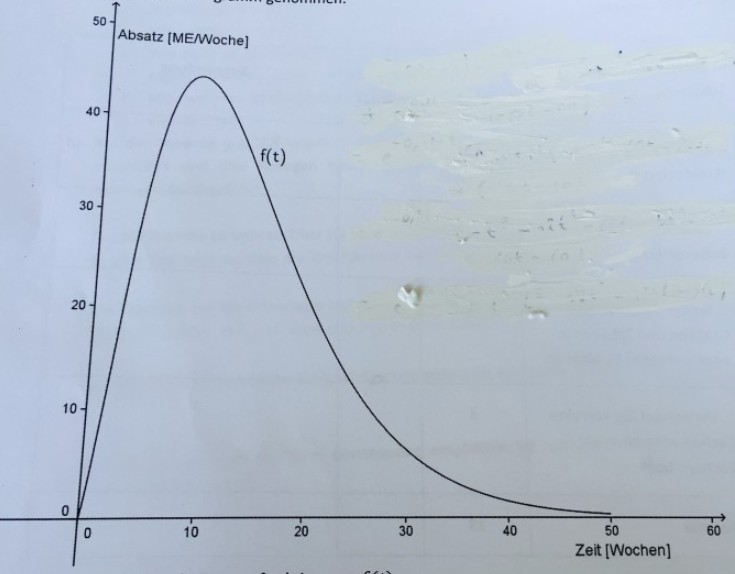
a) Berechnen Sie die Stammfunktion von \( f(t) \).

Lösung zum Weiterrechnen: \( F(t)=e^{-0,2 t+1} \cdot\left(-5 t^{2}-60 t-300\right) \).

b) Bestimmen Sie die abgesetzte Stückzahl bis zur 50. Woche.

c) Berechnen Sie, welcher Anteil am Gesamtabsatz bis zur 20. Woche gemacht wird.

d) Berechnen Sie, in welcher Woche ist der Absatz maximal ist.

Answer 1

b) Integriere f(t) von 0 bis 50

c) Integriere f(t) von 0 bis 20 und teile das Ergebnis durch das Ergebnis aus b)

d) Berechne: f '(t) = 0

Answer 2

a.) war, zumindest für mich, recht kompliziert ist mir aber gelungen.
Kann die Herleitung der Stammfunktion auch noch einstellen.

b.) Ist die Fläche unterhalb des Graphen von f
oder
F ( 50) - F ( 0 )
F ( t ) =(  - 5 * t^2 - 60 * t - 300 ) * e^{-0.2*t+1}

(  - 5 * 50^2 - 60 * 50 - 300 ) * e^{-0.2*50+1} -
( - 5 * 0^2 - 60 * 0 - 300 ) * e^{-0.2*0+1}
813.54

c.) F ( 20 ) - F ( 0 ) = 641.23
Anteil : 641.23 / 813.54

d.)
Es wird nach dem Extremum des Absatzes gefragt
f ( t ) = ( t^2 + 2t ) * e^{-0.2*t+1}
f ´ ( x ) = ( 2* t + 2 ) * e^{-0.2*t+1} + ( t^2 + 2t ) * e^{-0.2*t+1} * ( -0.2 )
f ´ ( x ) = e^{-0.2*t+1} * ( -0.2*t^2 - 2*0.2t + 2t + 2 )
f ´ ( x ) = e^{-0.2*t+1} * ( -0.2*t^2 + 1.6 * t + 2 )
e^{-0.2*t+1} * ( -0.2*t^2 + 1.6 * t + 2 )  = 0
-0.2*t^2 + 1.6 * t + 2  = 0  | pq-Formel oder quadratische Ergänzung
t = 9.1