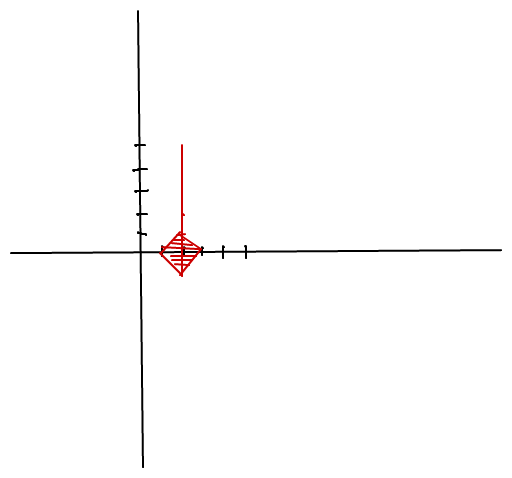
für die erste "Kugel"brauchst du alle Punkte, die von (2,2) in dieser Metrik
weniger als 1 entfernt sind. Für Punkte mit x-Wert 2 sind das alle
auf der Strecke (ohnen Endpunkte) von (2,1) bis (2,3) wegn
der Def. für x1=x2.
Ist aber der x-Wert eines Punktes nicht 2, dann ist ja bei
|y1|+|x2-x1|+|y2| schon der erste Summand gleich 2, also gibt
es in diesem Fall keine Punkte , die weniger als 2 von (2,2) entfernt
sind. Die ganze "Kugel" ist die genannte Strecke.
Bei Radius 2 ist es ähnlich, denn für x ungleich 2 ist der Abstand eines Punktes
von M immer > 2, also wieder die Strecke, nur diesmal von (2,0) bis (2,4)
bei r=3 wird es schon spannender. Erst mal die Strecke von (2,-1) bis (2,5) aber
dann auch noch Punkte mit x ungleich 2 und zwar solche mit
d( (2,2), (x,y) ) < 3
2 + |x-2| + |y| < 3
|x-2| + |y| < 1
|x-2| < 1- |y|
damit das überhaupt geht, muss |y| < 1 sein
und dann muss noch |x-2| , also der Unterschied zwischen x und 2
kleiner sein als dieses 1- |y|
z.B. für |y|=0,8 kann zwischen 1,8 und 2,2 liegen
oder für |y|=0,5 kann zwischen 1,5 und 2,5 liegen
oder für |y|=0,3 kann zwischen 1,3 und 2,7 liegen etc.
Ich versuche mal B3 zu zeichnen: