Mein Ansatz so ok?
Titel: Berechnen Sie für zwei Spielvarianten jeweils die Gewinnchancen für Peter und Paul. Alternierender und abbrechender Baum
Stichworte: wahrscheinlichkeit,urne,zurücklegen,stochastik
Aufgabe: Alternierender und abbrechender Baum
Unser Mathelehrer hat uns diese Aufgabe über die Weihnachtsferien aufgegeben, auch hat er weitere Arbeitsblätter die darauf aufbauen reingestellt die wir lösen können, dies ist allerdings freiwillig, ich würde mich aber gerne zumindest daran versuchen wollen. Nun zu den Aufgaben, wir haben jetzt Stochastik angefangen, allerdings hat uns der Lehrer nichts zu Alternierenden und abbrechenden Bäumen erzählt, er möchte das wir quasi selber Wege finden um auf die Lösungen zu kommen. Da ich aber gerne auch die weiteren Arbeitsblätter berechnen würde, möchte ich das verstehen damit ich nicht anschließend irgendeinen Mist zusammenrechnen tue, könnte mir jemand also erklären wie man die Aufgaben löst, dann kann ich diese Aufgaben als Muster nehmen und das auf die anderen Aufgaben anpassen.
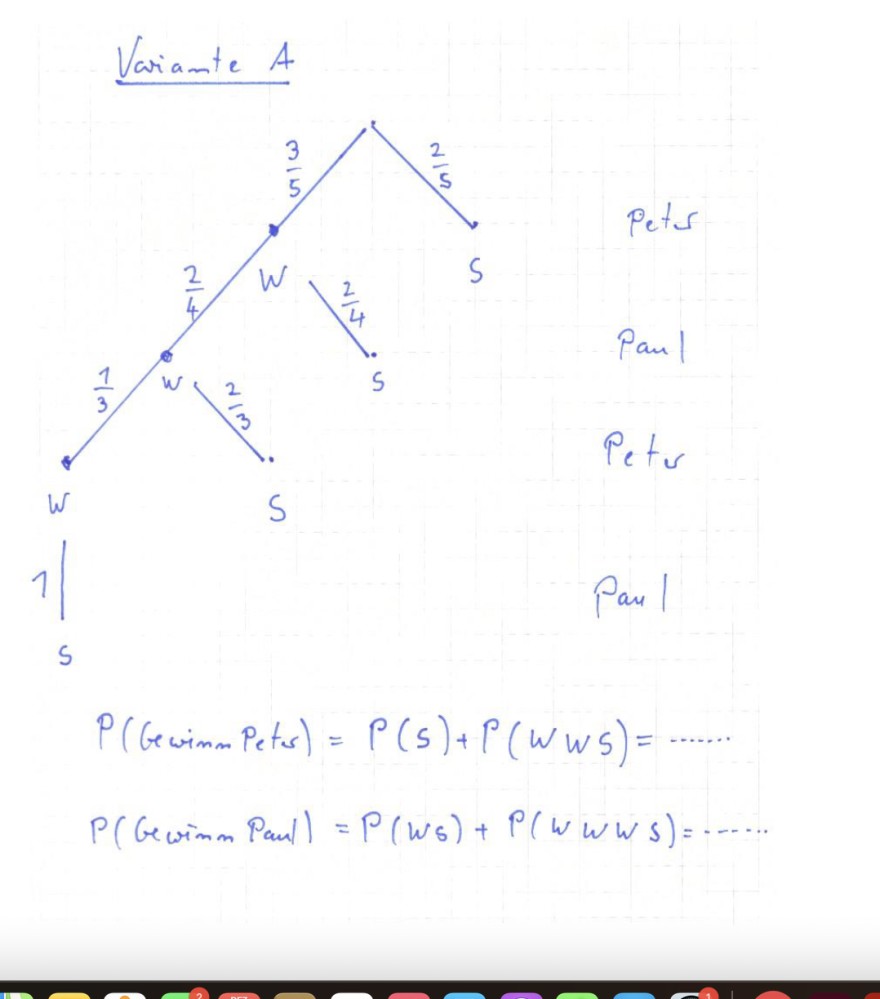
Im Folgenden ist eine Aufgabe mit zwei Varianten beschrieben. Der Lösungsweg für die Variante A ist mit vollständigem Baumdiagramm und Berechnungsansätzen ausgeführt.
Vervollständigen Sie die Berechnung zu Variante A.
Erarbeiten Sie eine vollständige Lösung zu Variante B (Baum und Rechnung).
Peter und Paul ziehen abwechselnd und ohne Zurücklegen je eine Kugel aus der abgebildeten Urne. Peter beginnt. Berechnen Sie für zwei Spielvarianten jeweils die Gewinnchancen für Peter und Paul.
Variante A: Wer zuerst eine schwarze Kugel zieht, gewinnt.
Variante B: Wer zuerst eine weiße Kugel zieht, gewinnt.
Text erkannt:
Varante \( A \)
Pets Panl Petor
Pan 1
s
\( P( \) Gewimm Pets \( )=P(s)+P(W W S)=\ldots \ldots \)
\( P( \) Gevinm \( P \) anl \( )=P\left(W_{s}\right)+P(W W W S)=\cdots \cdot \cdot \)