Höhe eines Kirchturms

Question

Um die Höhe eines Kirchturms zu bestimmen, hat man eine horizontale Standlinie von der Länge s= 65m abgesteckt, die auf den Turm zuläuft. In ihren Endpunkten erblickt man die Turmspitze unter den Erhebungswinkeln a= 49,5° und ß= 27°. Die Augenhöhe beträgt 1,60m. Wie hoch ist der Kirchturm?

Answer 1

Allgemeiner Ansatz der Höhenbestimmung von einer Standlinie aus

Gegeben sind a, α und β

γ = 180° - β

δ = 180°- α - γ = β - α

b = a / sin(δ) · sin(α) = a · sin(α) / sin(β - α)

h = b · sin(β)

h = a · sin(β) · sin(α) / sin(β - α)

h = 65 · sin(49.5°) · sin(27°) / sin(49.5° - 27°) = 58.64

58.64 + 1.6 = 60.24 m

Der Turm ist 60.24 m hoch.

Comments

:) Was ich noch nicht verstehe ist, wie man auf die Ansätze kommt. Ist das so eine normale Formel? Wenn ja, wie lautet diese? Und bei mir kommt im TR statt 58,64 ca. 22,4 raus. Woran liegt das?

Danke und viele Grüße

Thomas

---

Mache dir zunächst eine Skizze und versuche den Lösungsweg mal nachzuvollziehen.

Hast du den TR auch im Gradmaß stehen?

---

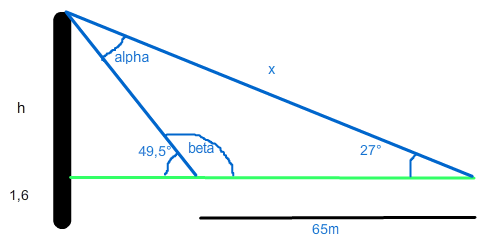
Also du bekommst beta also Ergänzungswinkel zu 49,5: β=180°-49,5°=130,5°. α ist dann die Ergänzung zur Innenwinkelsumme von 180° im Dreieck: α=180-27-130,5=22,5°.

Du bekommst jetzt die Länge x durch den Sinus-Satz heraus: 65/sin(α) = x/sin(β). Nach x aufgelöst ergibt sich:

x=129,16m. Jetzt kannst du die Höhe h bestimmen durch den Sinus in dem großen Dreieck:

sin(27)=h/x. Umgestellt ergibt sich: h=sin(27)*x=sin(27)*129,16=58,64m. Alles klar?