Aufgabe:
Lea verschläft etwa an jedem 20. Schultag (V); an jedem 10. Tag kommt sie zu spät (Z) zur Schule. Ihr Zuspätkommen beruht in 40 % aller Fälle auf dem Verschlafen.
a) Tragen Sie zunächst nur die gegebenen Wahrscheinlichkeiten an passender Stelle ein:

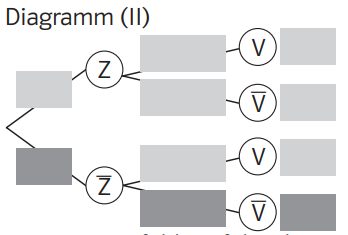
(Die für Teilaufgabe d) ergänzten Werte sind dunkler hinterlegt.)
b) Warum ist es hier günstiger, die Bearbeitung der Aufgabe mit einer Vierfeldertafel zu beginnen?
c) Erstellen Sie eine geeignete Vierfeldertafel,.
d) Welches der Baumdiagramme (I) oder (II) ist jeweils geeigneter, um folgende Frage zu beantworten? Ergänzen Sie das jeweilige Baumdiagramm entsprechend, um die gesuchte Wahrscheinlichkeit P zu berechnen. Runden Sie geeignet.
| Wie groß ist die Wahrscheinlichkeit, ... | (I)/(II) | P |
| … dass Lea zu spät kommt, wenn sie verschläft? |
|
|
| … dass Lea nicht verschlafen hat, wenn sie nicht zu spät ist? |
|
|
| … dass Lea zu spät kommt, obwohl sie nicht verschlafen hat? |
|
|
Ansatz/Problem:
Ich übe gerade für die ZAP. Wir sollten uns über bedingte Wahrscheinlichkeit informieren.