K(x) = 0.001·x^3 - 0.18·x^2 + 12.5·x + 84
E(x) = 6·x
a) Ermitteln Sie die Gewinnfunktion
G(x) = E(x) - K(x) = 6·x - (0.001·x^3 - 0.18·x^2 + 12.5·x + 84) = - 0.001·x^3 + 0.18·x^2 - 6.5·x - 84
b) Ermitteln Sie die Nutzenschwelle und Nutzengrenze (Hilfestellung: Bei x = - 10 liegt ein "mathematischer" Schnittpunkt der Funktion K(x) und E(x)
G(x) = 0
( - 1/1000x^3 + 9/50x^2 - 13/2x - 84) : (x + 10) = -1/1000x^2 + 19/100x - 42/5
- 1/1000x^3 - 1/100x^2
——————————
19/100x^2 - 13/2x - 84
19/100x^2 + 19/10x
——————————
- 42/5x - 84
- 42/5x - 84
——————————
0
-1/1000x^2 + 19/100x - 42/5 = 0
Lösen mit der Mitternachtsformel ergibt
x = 120 ∨ x = 70
Gewinnschwelle bei 70 und Gewinngrenze bei 120 ME
c) Bestimmen Sie die gewinnmaximale Ausbringungsmenge und das Gewinnmaximum
G'(x) = 0
- 0.003·x^2 + 0.36·x - 6.5 = 0
Lösen mit Mitternachtsformel ergibt
x = 97.86 ∨ x = 22.14
G(97.86) = 66.53
Wir haben den maximalen Gewinn von 66.53 GE bei einer Ausbringungsmenge von 97.86 ME
d) In welchem Intervall steigen die Kosten progressiv und in welchen degressiv?
Progressiv
K''(x) > 0
0.006·x - 0.36 > 0
x > 60
Degressiv
K''(x) < 0
0.006·x - 0.36 < 0
x < 60
e) Stellen Sie die Funktionsgleichung für die variablen Stückkosten auf und ermitteln Sie das Betriebsminimum!
kv(x) = 0.001·x^2 - 0.18·x + 12.5
kv'(x) = 0
0.002·x - 0.18 = 0
x = 90 ME
kv(90) = 4.4 GE
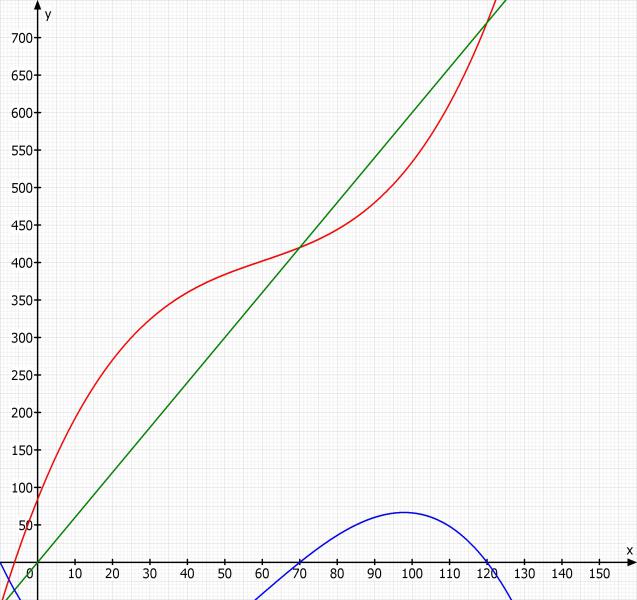
f) Stellen Sie die Funktionen E(x), K(x) und G(x) graphisch dar. Benutzen Sie dafür EIN Koordiantensystem und beschränken Sie sich auf den Deffinitionsbereich D = [0;150]