Aufgabe:
Sei \( s_{m} \) die Seitenlänge des regulären, den Einheitskreis umschreibenden, \( m \)-Ecks.
Bestimmen Sie eine Rekursionsvorschrift zur Berechnung von \( s_{2m} \) aus \( s_{m} \) und finden Sie damit eine Näherung für \( \pi=3.14159 \ldots \), die 2 richtige Nachkommastellen hat.
Hinweis: Betrachten Sie folgendes Bild:
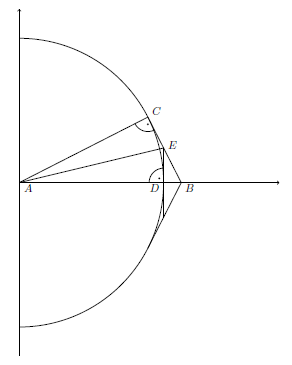
Dabei sind die Seitenlängen wie folgt:
\( l(\overline{A C})=l(\overline{A D})=1, \quad l(\overline{C B})=\frac{s_{m}}{2}, \quad l(\overline{D E})=\frac{s_{2 m}}{2} . \)
Ansatz/Problem:
Für mich sieht das aus, als könnte man mit dem Satz des Pythagoras rechnen, allerdings weiß ich nicht genau, was ich da machen muss.