Aufgabe:
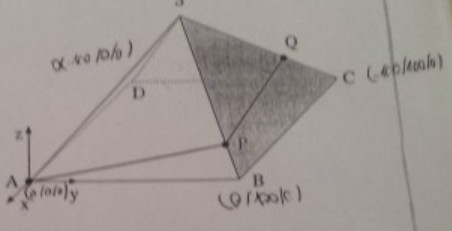
I. Geraden
a) Bestimmen Sie die Gleichungen der Geraden, in denen die vier Pyramidenkanten verlaufen.
b) Forscher vermuten, dass das Baumaterial über riesige Rampen, die sich längs der eingezeichneten blauen Strecken an die Pyramide lehnten, transportiert wurde.
Die erste Rampe hat im Punkt P \( 10 \mathrm{~m} \) Höhenunterschied erreicht. Bestimmen Sie P.
c) Die anschließende Rampe soll den gleichen Steigungswinkel besitzen.
Bestimmen Sie die Gleichung der entsprechenden Geraden.
In welchem Punkt Q endet diese Rampe?
In welchem Punkt erreicht die Rampe die Höhe von \( 15 \mathrm{~m} \) ?
d) In welchen Punkten durchstoßen die Pyramidenkanten eine Höhe von \( 20 \mathrm{~m} \)?
In welcher Höhe beträgt der horizontale Querschnitt der Pyramide \( 25 \mathrm{~m}^{2} \)?
II. Geradenschar
Vom Punkt T \( (50|-50| 100) \) fällt Licht in Richtung \( \left(\begin{array}{c}-1-a \\ 3-a \\ a-2\end{array}\right) \)
a) Zeigen Sie, dass vom Punkt T je ein Lichtstrahl auf die Punkte B und S fällt.
b) Zeigen Sie: Jeder Punkt der Kante \( \overline{BS} \) wird angestrahlt.
c) Bestimmen Sie den Schattenwurf der Kante BS in der x-y-Ebene.
Ansatz/Problem:
Von der ersten Aufgabe benötige ich bei Teilaufgabe c Hilfe. Mein Ansatz wäre, dass ich die Gerade mit dem Stützvektor OP und den Richtungsvektor PQ bilde und dann diese auf Schnittstellen mit der Gerade CS prüfe.