Aufgabe:
Finden Sie den Fehler im folgenden "Beweis", dass alle Winkel kongruent sind:
Im Viereck \( A B D C \) seien die Winkel \( \angle(A B D) \) und \( \angle(B D C) \) beliebig gewählt (durch Winkelabtragung zweier beliebiger gegebener Winkel) und \( A B \cong C D \) (durch Streckenabtragung). \( G \) sei der Schnittpunkt der Mittelsenkrechten von \( B D \) bzw. \( A C \). Dann ist \( G B \simeq G D \), da \( G \) auf der Mittelsenkrechten von \( B D \) liegt, \( G A \cong G C, \mathrm{da} G \) auf der Mittelsenkrechten von \( A C \) liegt und \( A B \cong C D \) nach Konstruktion. Folglich sind nach Kongruenzsatz [SSS] die Dreiecke \( \Delta(A, G, B) \cong \Delta(C, G, D) \) und insbesondere die Winkel \( \angle(G B A) \cong \angle(G D C) \) kongruent. Weiterhin ist das Dreieck \( \Delta(B, D, G) \) gleichschenklig und folglich die Winkel \( \angle(G B D) \cong \angle(G D B) \) kongruent. Also, schlussendlich, sind die Winkel \( \angle(A B D) \cong \angle(B D C) \) kongruent, was zu zeigen war.
Benutzen Sie Zirkel und Lineal oder eine Geometriesoftware, um mit der geometrischen Konfiguration zu experimentieren.
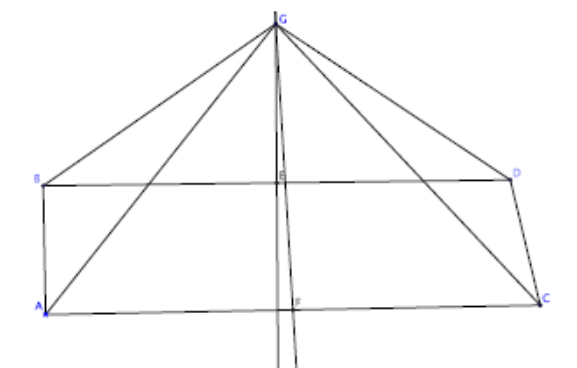
Ansatz/Problem:
Welches Viereck sollte ich am besten konstruieren, um den Fehler des Beweises zu erkennen?
Mit AB usw. sind Strecken gemeint, keine Geraden. Die Überstriche wurden weggelassen.
Ich habe durch Konstruktion herausgefunden, dass der Fall oben nur bei einem gleichschenkligen Trapez gilt. Alle anderen Vielecken widerlegen diese Behauptung. Wo aber liegt nun der Fehler im Beweis?
Und bei einem Rechteck und Quadrat sind die beiden Winkel auch gleich.