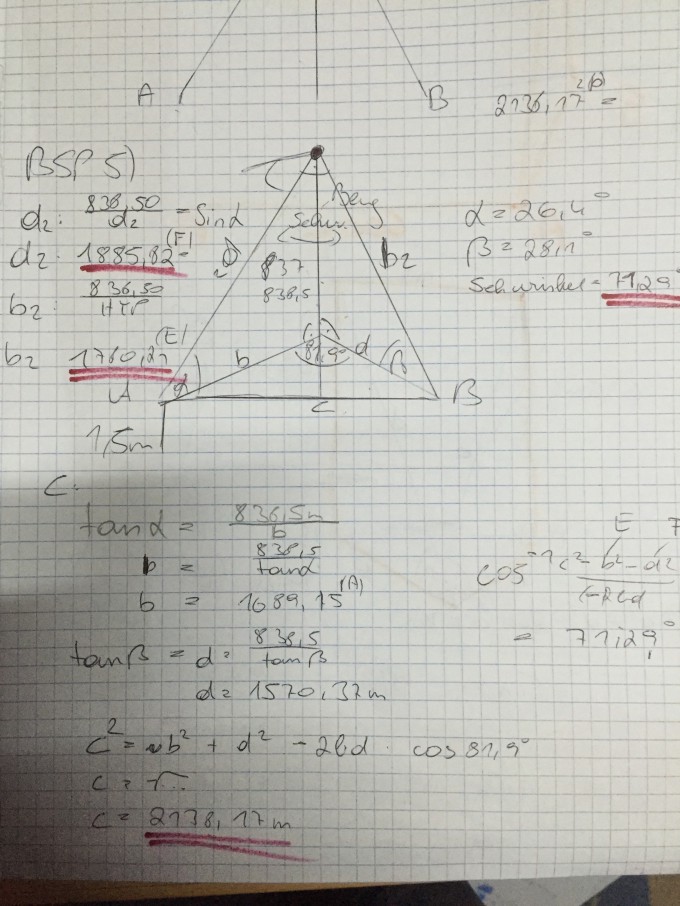
Zwei Orte A und B liegen – durch einen Morast getrennt – in einer Hochebene. Um ihre Entfernung zu bestimmen, werden von einem Berggipfel, der sich 837,0m über dieser Ebene befindet, Vermessungen zu A und B vorgenommen: Vom Gipfel aus sieht man den Ort A unter dem Tiefenwinkel a = 26,4° und nach Schwenken des Messinstruments um den Horizontalwinkel g = 81,9° den Ort B unter dem Tiefenwinkel b = 28,1°.
a) Fertige eine Skizze an und berechne unter Berücksichtigung einer Instrumentenhöhe von 1,5 m die Entfernung der Orte A und B. Unter welchem Winkel sieht man die Strecke AB von der Bergspitze aus?
b) Wie weit ist der Wanderer vom Ort B entfernt? Wie groß wäre diese Entfernung in einer Karte im Maßstab 1 : 50 000 einzutragen? (Ergebnis in cm, 1 Dezimalstelle)
Für a bekomme ich 2138,17 m und 71,29 Grad.
Für b 1,1 cm.
Bitte um Kontrolle