Regenrinne mit parbelförmigen Querschnitt soll 40 cm breit und 20 cm hoch sein.

Question

Thema quadratische Funktionen:

Aufgabe 1:

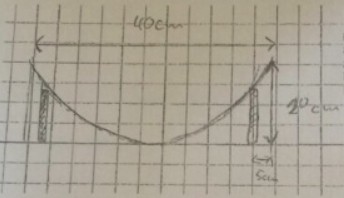
Eine Regenrinne mit parabelförmigem Querschnitt soll $40 \mathrm{~cm}$ breit und $20 \mathrm{~cm}$ hoch sein. Welche Höhe muss eine $5 \mathrm{~cm}$ vom Rand entfernte Stütze haben? Berechnen Sie.

Hinweis: Fertigen Sie zunächst eine Skizze an und legen Sie ein zweckmäßiges Koordinatensystem an. Bestimmen Sie dann eine Funktionsgleichung.

Aufgabe 2:

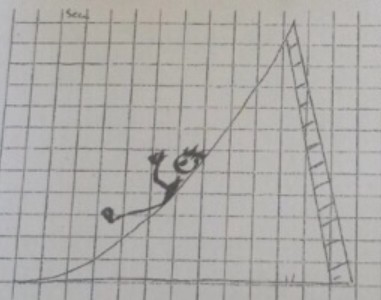
Eine Rutsche ist $2 \mathrm{~m}$ hoch und wie ein Parabelast geformt. Ihre Breite ist $1,8 \mathrm{~m}$. Alle $60 \mathrm{~cm}$ (waagerecht gemessen) sollen senkrechte Stützen angebracht werden. Wie lang müssen die Stützen sein, wenn das Ende der Rutsche $50 \mathrm{~cm}$ über dem Boden ist?

Hinweis: Zuerst eigene Skizze anfertigen - mit den Stützen.

Answer 1

zu Aufgabe 1:

Die Parabel f(x) = ax² geht durch den Punkt P(20 | 20).

f(20) = a*20² = 20 --> a = 1/20 = 0.05

f(x) = 0.05*x²

f(15) = 0.05*15² = 11.25 cm

zu Aufgabe 2:

Auch hier wieder f(x) = a*x²

Kennst du einen Punkt der Parabel wie in der vorherigen Aufgabe. Dann einsetzen und nach a auflösen. Mit der Funktion dann die Stützen berechnen.

Probier das zunächst mal selber.

Comments

Ich werde es versuchen. Können wir ein paar Sätze über quadratische Funktionen erläutern?

---

Schau dir folgende Videos an. Wenn dir die Videos den vermittelten Stoff gut vermitteln, solltest du über einen Lernzugang online nachdenken.

Siehe auch https://www.matheretter.de/wiki/quadratischegleichung