Berechnung des Fassinhaltes mit Hilfe der Keplerschen Fassregel

Question

Hi, ich habe folgende Aufgabe bekommen und würde mich riesig über das Ergebnis oder Hilfe freuen.

Folgendes:

Es geht um das große Heidelberger Fass. Anfangs betrug sein Fassungsvermögen ca. 228000 Liter, durch Eintrocknen des Holzes schätzt man sein Volumen heute auf 219000 Liter. Messungen sind auf Grund der Größe etc. sehr schwierig. Folgende Daten sind bekannt:

- Durchmesser des Grund- bzw. Deckkreises d1=5,75m
- In der Fassmitte beträgt der Durchmesser d= 6,10m
- Fasslänge beträgt etwa h=7,88m
- Wölbung von Grund und Deckkreis: Die Balken sind in der Mitte um ca. 12,5cm gegenüber dem Fassrand nach innen gewölbt.


Aufgaben:

a) Berechnen sie mittels geeigneter Methoden auf zwei verschiedene Wege einen möglichst genauen Näherungswert für den Fassinhalt. Berücksichtigen Sie dabei die Wölbung von Grund und Deckfläche.

b) Welcher Maximale bzw. minimale Fassinhalt würde sich ergeben, wenn man auf Grund von schwierigen Messbedingungen von einer Messgenauigkeit von +- 5cm ausgeht?


Kann mir da jemand helfen? Mir das erklären?

Danke.

Answer 1

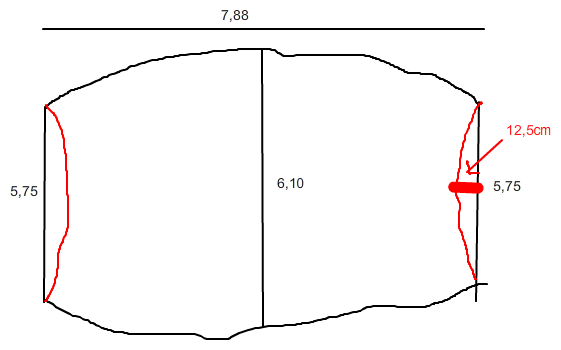
 Mit  Keppler-Fass-regel die Kreisflächen zu den Durchmessern5,75  6,10  und 5,75 ausrechnen
gibt  25,97m^2     29,22m^2  und   25,97m^2   
mit Kepplerformel  V = 1/6 * 7,88m * ( 25,97m^2   + 4*  29,22m^2  + 25,97m^2   )
= 230,29 m^3  = 230290 Liter.
Jetzt noch den Verlust durch die Wölbung abziehen.

2. Möglichkeit: mit Parabelbögen arbeiten.

Genauigkeit: alle Maße - 5m und dann alle Maße + 5cm nehmen. Gibt das minimale und das maximale Ergebnsi.