ich habe eine Aufgabe mit Messwerten und soll eine Regressionsgerade (Anstieg) erstellen bzw. berechnen. Ich habe die Messwerte tabellarisch notiert und die Diagramme erstellt. Ich bin mir nicht sicher, ob die erstellten Regressionsgeraden richtig sind.
Grüße,
Asterix
AUFGABEN.pdf (41 kb)
Tab. 1: Messtabelle
|
Probe |
E(535) nach10 min |
E(535) nach 20 min |
E (535) nach 60 min |
Frischmasse in g |
|
1 |
0,002 |
0,100 |
0,028 |
0,134 |
|
+Fe |
2 |
0,002 |
0,096 |
0,011 |
0,141 |
|
3 |
0,011 |
0,095 |
0,059 |
0,138 |
|
1 |
0,035 |
0,086 |
0,202 |
0,191 |
|
-Fe |
2 |
0,010 |
0,156 |
0,667 |
0,191 |
|
3 |
0,031 |
0,097 |
0,252 |
0,170 |
$$n={ E }_{ 535 }\cdot 2\cdot 0,0106l\cdot { 10 }^{ 9 }/22140\quad [nmol]$$
Tab. 2: 1. Berechnung
|
Probe |
10 min |
20 min |
60 min |
Frischmasse in g |
|
1 |
1,92 |
95,75 |
26,81 |
0,134 |
|
+Fe |
2 |
1,92 |
91,92 |
10,53 |
0,141 |
|
3 |
10,53 |
90,97 |
56,50 |
0,138 |
|
1 |
33,51 |
82,35 |
193,42 |
0,191 |
|
-Fe |
2 |
9,58 |
149,38 |
638,68 |
0,191 |
|
3 |
29,68 |
92,88 |
241,30 |
0,170 |
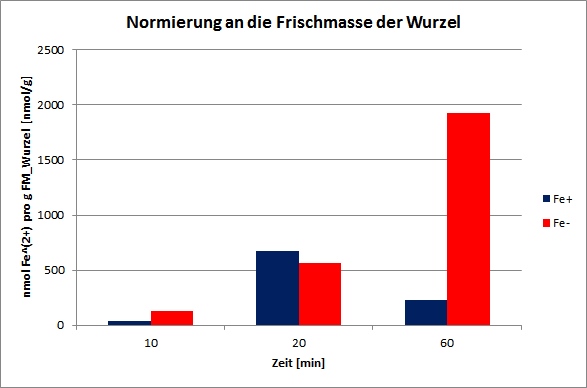
Normierung an die Frischmasse der Wurzel:
$$N=n/FM\quad (nmol\quad { Fe }^{ 2+ }\quad pro\quad g\quad { FM }_{ Wurzel })$$
Tab. 3: 2. Berechnung
|
Probe |
10 min |
20 min |
60 min |
|
1 |
14,33 |
714,55 |
200,07 |
|
+Fe |
2 |
13,62 |
651,91 |
74,68 |
|
3 |
76,30 |
659,20 |
409,42 |
|
1 |
175,45 |
431,15 |
1012,67 |
|
-Fe |
2 |
50,16 |
782,09 |
3343,87 |
|
3 |
174,59 |
546,35 |
1419,41 |
Tab. 4: Mittelwerte
|
10 min |
20 min |
60 min |
|
+Fe (N) |
33,75 |
675,22 |
228,05 |
|
-Fe (N) |
133,40 |
586,53 |
1925,32 |
$$A=\frac { \Delta \bar { N } }{ \Delta t } $$
Bedeutet das Δ, dass die Werte subtrahiert werden?:+Fe: 675,22-228,05-33,75=413,42-Fe: 1925,32-586,53-133,40=1205,39
t: 60-20-10=30
Nach der Formel Steigung für (+Fe): 413,42/30=13,78
Nach der Formel Steigung für (-Fe): 1205,39/30=40,18
Excel zeigt mir, aber andere Formeln an:(+Fe): y=96,655x+118,62
(-Fe): y=895,96x-916,17