Ich bin hier an drei Aufgaben wovon ich zwei bereits gelöst zu haben glaube.
Bei der dritten komme ich allerdings nicht weiter und brauche Hilfe.
(1) Gegeben sei die Funktion f (x, y ) = 2x² − 3xy + 2y² .
(a) Man berechne die kritischen Punkte sowie die Hesse-Matrix.
-Hier habe ich folgendes durch partielles Ableiten herausbekommen:
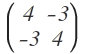
(b) Man entscheide für jeden kritischen Punkt, ob eine Minimalstelle, Maximalstelle oder ein Sattelpunkt vorliegt.
-Hier habe ich die Hesse-Matrix minus die Einheitsmatrix mit Skalar berechnet und kam auf das charakteristische Polynom:
2λ²-16λ=0
-Deshalb Null-gesetzt, damit ich die Nullstellen herausbekomme die bei
0 und 8 sind.
-Ich hoffe bis hier her habe ich richtig gerechnet! (Falls nicht, verbessert mich bitte!)
-Weiterhin habe ich die Determinante D berechnet und 32 herausbekommen.
****Ab hier weiß ich nicht weiter.****
(c) Welche Punkte kommen als Extremstellen der Funktion f unter der folgenden Nebenbedingung infrage
g(x, y ) = x² + y² = 1?