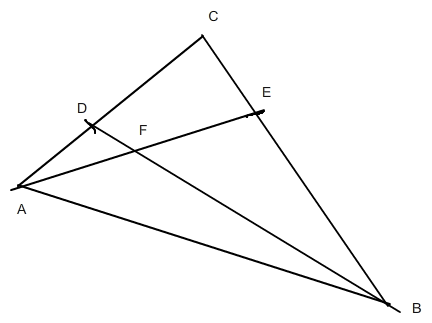
Ich lasse mal die Pfeile weg und schreibe so:
Es ist BF = x * BD Das x kennst du erst mal nicht. aber BD = BA + AD = -AB + (1/3)* AC also
BF = x * -AB + (1/3)* AC = - x * AB + (1/3)* x* AC
und BF = (3/4)* BC + y * EA und EA = (1/4) * BC + CA = (1/4) * ( BA + AC ) + CA , also
BF = (3/4)* BC + y * ( (1/4) * ( BA + AC ) + CA )
= (3/4)* ( BA + AC ) + (1/4)*y * BA + (1/4)*y * AC + y * CA
= (3/4)* BA +(3/4)* AC + (1/4)*y * BA + (1/4)*y * AC + y * CA
= -(3/4)* AB - (1/4)*y * AB +(3/4)* AC + (1/4)*y * AC - y * AC
= ( -(3/4) - (1/4)* y ) * AB + ( (3/4) - (3/4)*y ) * AC
Weil AB und AC lin. unabh. sind, muss die Darstellung von BF eindeutig sein, also
ist - x = -(3/4) - (1/4)* y und (1/3)* x = (3/4) - (3/4)*y
Damit kannst du x und y ausrechnen und hast deine Lin.komb.