Anwendung der Parabel. Flugbahn eines Golfballs ohne Luftwiderstand.

Question

brauche hilfe bei dieser Aufgabe.schreibe nächste woche eine mathe Klausur und weiss nicht wie das geht und mein Lehrer meinte es kommen solche ähnlichen Aufgaben :(( könnt ihr mir helfen oder die Rechnung aufschreiben damit ich das irgendwie nachvollziehen kann.

Danke danke danke danke,

euer Einstein :****

Aufgabe:

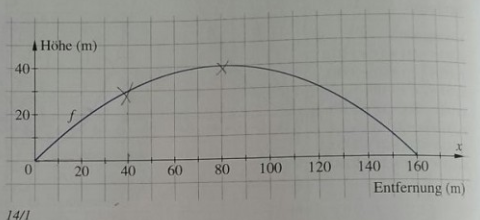
Flugbahnen wie die eines Golfballes haben, wenn man vom Luftwiderstand absieht, die Form von Parabeln. Die Abbildung zeigt die Flufbahn eines Golfballs, der im Punkt (0|0) abgeschlagen wurde.

a) Geben Sie die Scheitelpunktform der dargestellten Flugbahn an und zeigen Sie durch Ausmultiplizieren, dass die Gleichung der Flugbahn auch durch f(x) = -\( \frac{1}{160} \) • x² + x angegeben werden kann.

b) Berechnen Sie die Höhe des Balls nach 100 m. Bei welcher Entfernung vom Abschlag hat der Ball die gleiche Höhe?

c) Berechnen Sie, in welcher Entfernung vom Abschlag der Ball eine Höhe von 20 m erreicht.

Answer 1

f(x) = - 40/80^2·(x - 80)^2 + 40 = x - x^2/160

Passt also

b) f(100) = 37.5

x = 60 [Folgs aus der Achsensymmetrie zu x = 80]

c) f(x) = 20 --> x = 23.43

Comments

Wie kommst du auf:

$$ a=-\left(\frac{40}{80}\right)^2$$

a ändert sich nicht es muss nur der Scheitelpunkt:

$$ S(d|e)$$

eingesetzt werden oder täuscht mich etwas oO.

---

Öffnungsfaktor:

- 40 / 80^2

Man geht vom Scheitelpunkt 40 nach unten wenn man 80 nach rechts oder links geht.

Und es heißt NICHT -(40/80)^2

---

Und es ist letztendlich doch wieder \(a=-\frac{1}{160}\) ;-)

Aber so hab ich noch gar nicht darüber nachgedacht :-)

---

Die Formel für den Öffnungsfaktor findet man auch komischerweise in keinem Lehrbuch und in keiner Formelsammlung. Dabei ist das so einleuchtend, wenn man Parabeln versteht, das man das unbedingt mit zur Scheitelpunktform lehren sollte.

Steigung bei linearen Funktionen

m = (y1 - y2) / (x1 - x2) ; Die Benennung der zwei Punkte ist egal.

Öffnungsfaktor bei quadratischen Funktionen

a = (y1 - y2) / (x1 - x2)^2 ; Der Punkte (x2 | y2) muss hier der Scheitelpunkt sein. Ansonsten erhält man ein verkehrtes Vorzeichen.

Man sollte erkennen das die Formeln fast gleich aussehen. Daher ist es nicht wild, das wenn man die erste ohnehin kennen muss auch die zweite gleich mitlernt.

Answer 2

a)

$$f\left( x \right) \quad =\quad a(x-d)^{ 2 }+e\\ \quad \quad a\quad =\quad -\frac { 1 }{ 160 } \\ \quad \quad d\quad =\quad 80\\ \quad \quad e\quad =\quad 40$$

b)

$$f\left( 100 \right) \quad =\quad y\quad =\quad f\left( { x }_{ 2 } \right) \\ { x }_{ 2 }\quad =\quad d-(100-d)$$

c)

$$f\left( x \right) =20\Leftrightarrow f\left( x \right) -20=0\\ \Rightarrow { x }_{ 1,2 }=\frac { -b\pm \sqrt { { b }^{ 2 }-4ac }  }{ 2a }  $$