Gleichungen der beiden Tangenten an den Graphen von f mit f(x)= 1/8x³mal(x+4), die durch P(2/6) gehen

Question

Das sind 2 Aufgaben die ich überhaupt nicht verstehe obwohl ich eigentlich gut in Mathe bin.
Es wäre nett wenn mir die jemand erklären oder machen würde und vielleicht mit Paint oder irgendeinen anderen Programm wo man das deutlich sehen kann. Die Zeichnung hab ich schon gemacht für die 1 Aufgabe aber das hat mir nicht weiter geholfen.

Nr 1.
Vom Punkt P(2/5) werden die Tangenten an den Graphen von f mit f(x)= -1/2x³+3/2x+2 gelegt. Bestimmen Sie die Gleichung dieser Tangenten und die Berührpunkte.

Nr 2.
Bestimmen Sie die Gleichungen der beiden Tangenten an den Graphen von f mit f(x)= 1/8x³mal(x+4), die durch P(2/6) gehen.

Answer 1

Nr 1.
Vom Punkt P(2/5) werden die Tangenten an den Graphen von f mit f(x)= -1/2x³+3/2x+2 gelegt. Bestimmen Sie die Gleichung dieser Tangenten und die Berührpunkte.

Ansatz Tangentengleichung

t: y = mx + q

P einsetzen 5 = 2m + q. Also: q = 5-2m

t: y = mx + 5 -2m

y ' = m

f(x) = -1/2 x^3  + 3/2x + 2

f '(x) = -3/2 x^2 + 3/2

Berühren heisst : Funktionswert und Steigung gleich im Berührungspunkt B(xB|yB)

m = -3/2 xB^2 + 3/2

m - 3/2 = - 3/2 xB^2
m = 3/2 - 3/2 xB^2

yB = -1/2 xB^3 + 3/2xB + 2 = mxB + 5 - 2m

m einsetzen (rechter Teil)

 -1/2 xB^3 + 3/2xB + 2 = (3/2 - 3/2 xB^2) xB + 5 - 2(3/2 - 3/2 xB^2)

 -1/2 xB^3 + 3/2xB + 2 = 3/2 xB - 3/2 xB^3 + 5 - 3 + 3 xB^2

xB^3 - 3xB^2 = 0

xB^2(xB-3) = 0

2 Lösungen: xB1 = 0 und xB2 = 3.

Nun zu beiden noch yB und m  und q berechnen

1. Lösung: xB1 = 0, m1 = 3/2, t: yB1= -1/2 xB1^3 + 3/2xB1 + 2 = 2, q1 = 5-2m1 = 2

t1: y = 3/2x + 2, P1(0|2)

2. Lösung: xB2 = 3, m2 = 3/2 - 3/2 * 9 = -12, t: yB2= -1/2 *3^3 + 3/2 *3 + 2 = -7, q2 = 5-2m2 = 29

t2: y = -12x + 29, P2(3|-7)

Kontrolle und allfällige Korrektur nach Skizze mit Funktionsplotter:

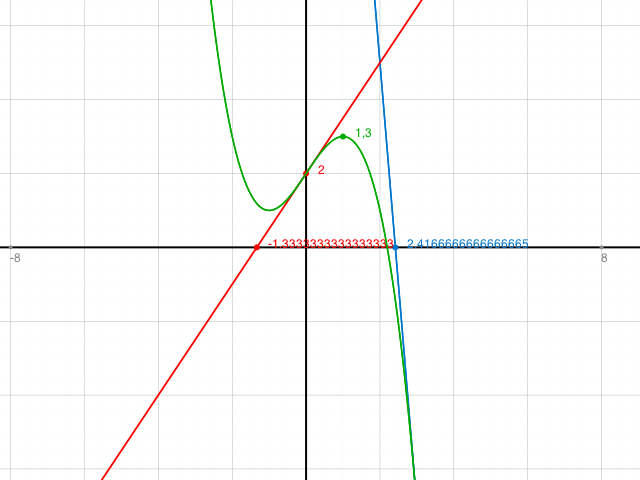
Scheint zu passen.

Nr2.
Bestimmen Sie die Gleichungen der beiden Tangenten an den Graphen von f mit f(x)= 1/8x³mal(x+4), die durch P(2/6) gehen.

Das geht nun vom Prinzip her wieder gleich. Rechne einfach mit f(x)  = 1/8 x^4  + 1/2 x, damit die Ableitung richtig rauskommt. Versuch das mal.

Anmerkung: Du hattest da noch das Stichwort 'Normalen'. Das hat aber mit dieser Aufgabenstellung nichts zu tun (?)

Comments

Dankeschön =)

Bei dir Nr 2 muss ich erst die Formel aus multiplizieren und dann die Ableitung davon machen?

---

Ja genau. Sonst musst du ja die Produktregel benutzen. Das ist umständlicher.

---

Ich glaube ich habe bei diesen Schritt ein Fehler gemacht.

m einsetzen (rechter Teil)

 

Nr.2

Ich habe am Schluss das raus und weiß jetzt nicht wie ich fortfahren soll.

3x² - 3/8x^4 -6=0

---

Das ist eine biquadratische Gleichung.

3x² - 3/8x⁴ -6=0          |:3

-1/8 x^4 - x^2 - 2 = 0

x^4 - 8x^2 + 16 = 0

Substitution x^2 =  u

u^2 - 8u + 16 = 0

(u-4)^2 = 0

u = 4

rückwärts substituieren: x = ± 2

Geht auf jeden Fall auf und du bekommst zwei x-Werte.

Answer 2

Vom Punkt P\((\blue{2}|\red{5})\) werden die Tangenten an den Graphen von f mit \(f(x)= -\frac{1}{2}x^3+\frac{3}{2}x+2\) gelegt. Bestimmen Sie die Gleichung dieser Tangenten und die Berührpunkte.

Die Berührpunkte haben die Koordinaten \((x|-\frac{1}{2}x^3+\frac{3}{2}x+2)\)

\(f'(x)= -\frac{3}{2}x^2+\frac{3}{2}\)

\(\frac{-\frac{1}{2}x^3+\frac{3}{2}x+2-\red{5}}{x-\blue{2}}=-\frac{3}{2}x^2+\frac{3}{2}\)

\(\frac{-\frac{1}{2}x^3+\frac{3}{2}x-3}{x-\blue{2}}=-\frac{3}{2}x^2+\frac{3}{2}\)

\(x_1=\green{0}\)   \(y_1=\orange{2}\)

\(x_2=3\)  \(y_2=-7\)

\(f'(0)= \frac{3}{2}\)

Tangentengleichungen mit der Punkt-Steigungsform der Geraden:

\(\frac{y-\orange{2}}{x-\green{0}}=\frac{3}{2}\)

1.)

\(y=\frac{3}{2}x+2\)

Analog die 2. Tangente

Comments

Viel Spaß weiterhin bei deinen Ausgrabungsarbeiten. Du gräbst ganz schön tief, magne et assidue effossor! :))