f´(x)= 0,75x2-6x+3a ✓
f´´(x)= 1,5x-6 ✓
f´´´(x)= 1,5 ✓
Du setzt die erste Ableitung gleich 0:
f´(x)= 0,75x2-6x+3a = 0 Ι:0,75
⇔ x2 - 8x + 3a = 0
⇔ x2 -8x +42 -42 +3a = 0
⇔ (x-4)2 -16 + 3a = 0 Ι+16 -3a
⇔ (x-4)2 = 16 - 3a Ι√ (a muss kleiner als 16/3 sein, ansonsten steht etwas
⇔ x-4 =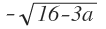 ∨ x-4 =
∨ x-4 = 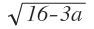 Negatives unter der Wurzel -> würde nicht gehen
Negatives unter der Wurzel -> würde nicht gehen
⇔ x = 4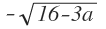 ∨ x = 4+
∨ x = 4+ 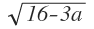 -> es gibt keine Extremstellen für a größer als 16/3)
-> es gibt keine Extremstellen für a größer als 16/3)
so weit, so gut, aber du darfst nicht einfach quadrieren!!
Hinreichende Bedingung:
f´´(4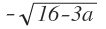 )= 1,5*(4
)= 1,5*(4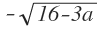 )-6= 1,5* 4 -1,5*
)-6= 1,5* 4 -1,5*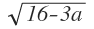 -6 = -1,5*
-6 = -1,5*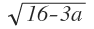
=> f'' (x1) < 0 --> Maximum bzw. Hochpunkt
f´´(4 + 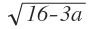 )=1,5*(4+
)=1,5*(4+ 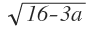 ) = 1,5*4 + 1,5*
) = 1,5*4 + 1,5* 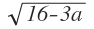 -6 = 1,5 *
-6 = 1,5 * 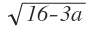
=> f''(x2) > 0 --> Minimum bzw. Tiefpunkt
dann in die Ausgangsfunktion eingegeben ergibt ✓
H(x1 Ι f(x1) )
T(x2 Ι f(x2) )
Jetzt setze ich mich an die zweite Aufgabe :)
Hoffe, es ist verständlich :)