Das X ist die nächste Zahl dieser Reihe und soll von euch ermittelt werden.

Question

46 - 36,5 - 28 - 27,5 - 23,3 - 23,1 - X

Das X ist die nächste Zahl dieser Reihe und soll von euch ermittelt werden.

Vielleicht hat ja jemand eine Idee

Answer 1

Auch wenn die Eingabe unüblich ist (Trennzeichen von Feldern ist nicht Minus sondern Komma oder ; oder | ), gibt es ohne Randbedingungen (Einschränkungen) bei endlichen Folgen IMMER UNENDLICH viele mögliche Algorithmen!

46, 36.5, 28, 27.5, 23.3, 23.1 ergibt bei http://www.gerdlamprecht.de/Mittelwerte.html

das Interpolationspolynom (unten auf der Seite):

46+x*2777/600-pow(x,2)*6587/240+pow(x,3)*4069/240-pow(x,4)*949/240+pow(x,5)*127/400

=(55200+x*(5554+x*(-32935+x*(20345+x*(381*x-4745)))))/1200

was der Iterationsrechner leicht berechnen kann:

http://www.gerdlamprecht.de/Roemisch_JAVA.htm#(55200+x*(5554+x*(-32935+x*(20345+x*(381*x-4745)))))/1200@Ni=0;@N@Bi]=Fx(i);@Ni%3E8@N0@N0@N#

ergibt

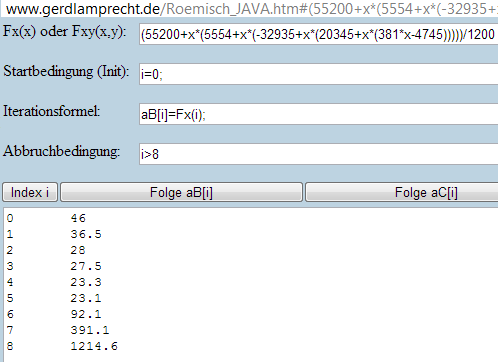
Ich kenne über 300 weitere Funktionen, die alle per Restpolynom wieder diese 6 Anfangsglieder haben, ABER anders fortgesetzt werden...

Dann gibt es Nachkommastellen-Algorithmen und Iterations-Algorithmen...

Betrachten wir das 10fache um das Dezimaltrennzeichen wegzubekommen:

460, 365, 280, 275, 233, 231

0.460365280275233231... ergibt unendlich viele Möglichkeiten:

1911254299/4151603913  =0.460 365 280 275 233 231 287 302 720 104 166 ...

691149721*Pi/4716495746=0.460 365 280 275 233 231 432 907 655 860 339 ...

Bei Interesse an weiteren Algorithmen melde Dich einfach.

Comments

Auch schön:

http://www.gerdlamprecht.de/Roemisch_JAVA.htm#10+x*581/2-@Px,2)*284+@Px,3)*127/2@NaB=Array(460,%20365);a=-85;@N@Bi+2]=@Bi+1]+a;a+=Fx(i+1);@Ci]=@Bi]/10;@Ni%3E8@N0@N0@N#

---

Da ich scheinbar nicht verstanden wurde:

§1: ohne Randbedingungen gibt es unendlich viele mögliche Fortsetzungen

§2: mit der Randbedingung "primitivstes Interpolationspolynom" lautet das nächste Glied: 92,1

§3: Randbedingung "primitivster Nachkommastellen-Algor. aus Bruchfunktionen mit 10 stelligen Nenner" lautet das nächste Glied:  28,7

§4: eine der primitivsten Nachkommastellen-Algorithmen mit Pi ergibt das nächste Glied 43,2

...

Dann gibt es noch zig weitere Algorithmen, Funktionen und jeder A. selbst kann beliebig kompliziert oder mit anderen A. verbunden werden.

Allein in Pi ist die 18 stellige Zahlenfolge etwa alle 40400000000000000000 Stellen zu finden

(vergl. http://www.gerdlamprecht.de/BisZuWelcherNKalleStringKombi.htm )

und da Pi unendlich viele Stellen hat -> gibt es allein für diesen A. unendlich viele mögliche "nächste Glieder"

---

Danke für die ausführliche Antwort. Doch das verstehe ich schon.

Ich dachte bei meiner Antwort , das es um Schulstoff geht (bis zum Abitur)

(arithm., geometrische oder unendliche geometrische Reihen)

Offensichlich ist es entweder eine Aufgabe aus dem Statistikbereich  oder Forschungsbereich ,

oder es sollte eine Knobelaufgabe sein.

---

Der Hinweis auf Statistik ist gut!

§5: Da gibt es die nichtlineare Regression: deutet auf fallende Exponentialfunktion hin.

Zusammen mit Ausgleichspolynom und Ränder-Abflachung (gegen Überschwingen des Ausgleichspolynoms) ergibt:

http://www.gerdlamprecht.de/Roemisch_JAVA.htm#x*4841857713/26513194-@Px,2)*24684934603/79341261+@Px,3)*9951672639/56659939-@Px,4)*3573385548/88995577+@Px,5)*244100147/76210389@Ni=0;@N@Bi]=round(248.8583974*exp(-5.493506359e-1*i)+211.1416026+Fx(i)*(atan((5.2-i)*1e3)/PI+1/2))/10;@Ni%3E8@N0@N0@N#

das nächste Glied: 22,1

Answer 2

Ich kann keine Gesetzmäßigkeit finden.

Deshalb kann das nächste Glied nicht ermittelt werden.

Comments

Leider doppelt falsch:

1. nicht keine sondern unendlich viele mögliche Gesetzmäßigkeiten (Algorithmen), wenn Randbedingungen fehlen

2. Nur weil Du keine G. gefunden hast, bedeutet das nicht logischerweise, dass es keine gibt.

---

Und wie lautet dann Deiner Meinung nach dieses Glied?

Eine richtige Antwort ist das ja  nicht.

:-)

---

Antwort im Kommentar meines Beitrages.

Bitte nicht als Kritik sehen -> es ist alles nur trockene Mathematik -> und die ist ohne Randbedingungen grenzenlos...

Answer 3

Liste der Seenotrettungsboote. Länge der Schiffsklassen... nächste Zahl ist 20,00