Winkelfunktionen. Bestimmen Sie sin(9/4π)

Question

haben ein neues thema angefangen und ich habe irgendwie große schwierigkeiten es zu begreifen obwohl ich in mathe nicht schlecht bin

also aufgabe ist gegeben

Bestimmen Sie: sin(9/4π)

Kann mir bitte jemand erklären was ich da machen muss?

Comments

Einfach in den Taschenrechner eingeben :)

Oder sollt ihr im Kopf rechnen?

---

ohne Taschenrechner :/

Answer 1

Wenn der Bruch 9/4 ist, also sin(9/4 π) = sin(9/4 *π), dann:

sin(9/4*π) = sin(8/4*π + 1/4*π) = sin(2*π + 1/4*π)

Einmal um den Kreis ist 2 π und dann noch mal 1/4 π, also einen Achtelkreis. Der Sinus ist also ≈ 0,707.

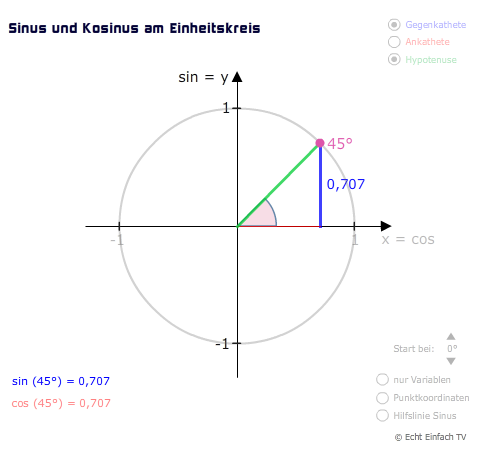
Hilfreich ist, wenn du weißt, dass 2 π = 360°. Dann sind 9/4 π = 405°.

Bzw. sin(9/4 *π) = sin(8/4 *π + 1/4 π) = sin(2*π + 1/4 π) = sin(360° + 45°) = sin(45°) ≈ 0,707

 

Mehr zum Thema siehe auch Video:

https://www.matheretter.de/wiki/einheitskreis

 

Wenn du keinen Taschenrechner zur Hand hast, kannst du für sin(45°) = √2 : 2 schreiben. Warum? Antwort: Stell dir das Dreieck nach unten gespiegelt vor, dann ergibt sich ein großes Dreieck mit einem Winkel von 90° statt 45°. Also rechtwinklig. Zwei Seiten sind 1 Einheit lang und die dritte lange Seite lässt sich nun per Satz des Pythagoras bestimmen: y² = 1² + 1², also Wurzel ziehen und wir erhalten:

y² = 1² + 1²
y = √(1² + 1²)
y = √(1 + 1)
y = √2

Wir wollen jedoch nur die Hälfte der Strecke, also teilen wir noch :2 und erhalten: sin(45°) = √2 :2

Dies wird im folgenden Video auch noch mal erklärt und grafisch verdeutlicht:

Answer 2

Es eigentlich wie jane schon sagt.

Entweder man hat eine Tabelle oder den Taschenrechner. Es gibt allerdings markante Werte, die man kennen sollte.

 

Dazu gehören auf jeden Fall:

sin(0)=0

sin(π/2)=1

sin(π)=0

sin(3/2*π)=-1

 

Und dann fängt es wieder von vorne an. Leicht zu merken, wenn man sich den Sinus schnell zeichnet ;).

 

Für uns gilt also der letzte Fall, denn 9/6=3/2 -> sin(9/6*π)=-1.

 

Grüße

Comments

Sry, verlesen. 9/4π ist gesucht^^.

 

Siehe Antwort von "einfachtv".

Answer 3

 

Das folgende Video erklärt Sinus uns Cosinus.

https://www.matheretter.de/wiki/einheitskreis

Du rechnest im Kopf wohl die Winkel besser auf Grad um

2π =^      360°

π = 180°

π/4 = 45° etc.

Jetzt kannst du den Sinuswert am Einheitskreis bestimmen.

sin(9/4π) = sin(2π + π/4) 

          |Sinus ist 2π-periodisch

= sin(π/4) 

             |in Grad

= sin(45°) 

            | halbes Quadrat mit Diagonale 1. 

            | Nach Pythagoras 2s^2 = 1

           | Seitenlänge s = 1/√2

= 1/√2

Answer 4

Das war damals mein Teil der Präsentation zu dem Thema:

Ich weiß ja noch nicht, welches Vorwissen bereits vorhanden ist, aber ganz unten steht auf jeden Fall der mathematische Beweis für die Fragestellung hier.

Die enthaltenen Skizzen sind aufgrund der Skalierung nicht mehr ganz so gut so erkennen, aber ich hoffe, das ist alles nachvollziehbar. :)