Hallo. Wir sollen das Minimalpolynom folgender Matrix bestimmen und wollte fragen ob meine Vorgehensweise richtig ist:
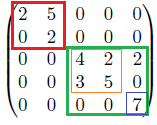
Diese Matrix ist in Blockgestalt, daher kann man das MP der beiden Blöcke A(rot) und B(grün) einzeln bestimmen. Wenn ein Eigenwert sowohl in Block A, als auch in Block B auftaucht, wäre das Minimalpolynom der Gesamtmatrix M gleich dem kleinsten gemeinsamen Vielfachen der Minimalpolynome (zum entsprechenden Eigenwert) der Blöcke A&B.
Nun berechne ich die Eigenwerte des Blocks A: 2, 2
Rechne ich nun (BlockA-2Id) erhalte ich eine Nullzeile (EDIT Lu), der Rang ist also 1. Da die Dimension der Matrix 2 ist, wäre die Dimension des Kerns 1 (Rangsatz). Da die dim(Ker) gleichzeitig die geometrische Vielfachheit des zugeordneten Eigenwerts angibt, kann es nur einen Jordanblock der Größe 2x2 geben. Somit lautet das MP des Blocks A: (t-2)^2
Meine erste konkrete Frage: SInd diese Überlegungen mathematisch korrekt?
Alternativ sollte man (BlockA-2Id) berechnen können und den Rang notieren (hier:1); anschließend berechnet man (BlockA-2Id)^2 und überprüft, ob der Rang abgenommen hat. Wäre der Rang immer noch 1, wäre das MP: (t-2) . Da der Rang jedoch erneut abgenommen hat (hier Nullmatrix -> Rang 0) lautet das MP des Blocks A: (t-2)^2
Meine zweite Frage: Sind diese Überlegungen mathematisch korrekt?
_______
Beim Block B geht man analog zu Block A vor:
Den ersten EW kann man ablesen (blaues Kästchen), wegen dem "Nullblock" in der dritten Spalte. Anschließend die EW des orangenen Kästchens berechnen. EW; 2,7,7
Die 2 kann man ignorieren (wg. MP(A), kgV...). Nun (BlockB-7Id): Rang=2, Dim=3 -> dim(Ker)=1
MP(B): (t-2)(t-7)^2
->MP der Matrix M: (t-2)^2 (t-7)^2
Entschuldigt den ausschweifenden Text, aber ich würde gerne wissen, ob meine grundsätzliche Vorgehensweise - insbesondere die Berechnung über die Dimension des Kerns (geoV) korrekt ist. Das finde ich persönlich einfacher (und schneller zu berechnen), als (M-xId)^n zu berechnen und zu schauen, ab wann der Rang nicht mehr abnimmt.
Vielen Dank, wenn sich jemand die Mühe macht, meine Fragen zu beantworten!