um eine Funktion abzuleiten benötigst du den Differentialquotienten.
Dieser lautet:
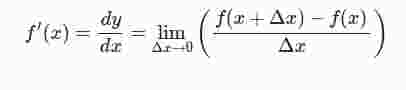
f'(x) bedeutet das die Funktionsgleichung einmal abgeleitet wird.

heißt das wir die Funktion y nach x ableiten. (y ist in diesem Fall eine andere Darstellung für f(x)).
Der Grenzwert einer Funktion kannst du dir folgendermaßen vorstellen:
Stellt man zum Beispiel die Funktion y = 1 + e-x grafisch dar, so kann man vermuten, dass sich die Funktionswerte für x → ∞ dem Wert 1 nähern. Wie den Grenzwert einer Folge kann man auch den Grenzwert einer Funktion mithilfe der ε-Umgebung beschreiben. Zeichnet man symmetrisch um den vermuteten Grenzwert g = 1 einen Streifen der Breite 2ε, so kann man eine Stelle x0 angeben, ab der alle Funktionswerte in diesem Streifen liegen.
Es gilt:

Den wenn du für x eine Zahl wie z.B. 3, 4, 20 , einfügst, so merkst du, dass e-x immer näher an 0 herankommt. Das würde wiederrum heißen, dass 1 + 0 = 1 ist.
~plot~1 + e^{-x};1.2;0.8~plot~
Der Bereich, welcher hier von zwei konstanten Funktionen eingeschlossen wird wird als ε-Umgebung bezeichnet.
Nun zur Aufgabe:
Wir setzen in den Differentialquotienten ein
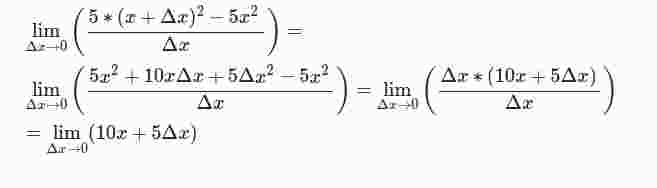
Wie du siehst wird die binomische Formel bei

angewandt.
Nun wird Δx zu 0. Daraus folgt:

Im Grunde genommen gilt für eine Ableitung der Potenzfunktion:
