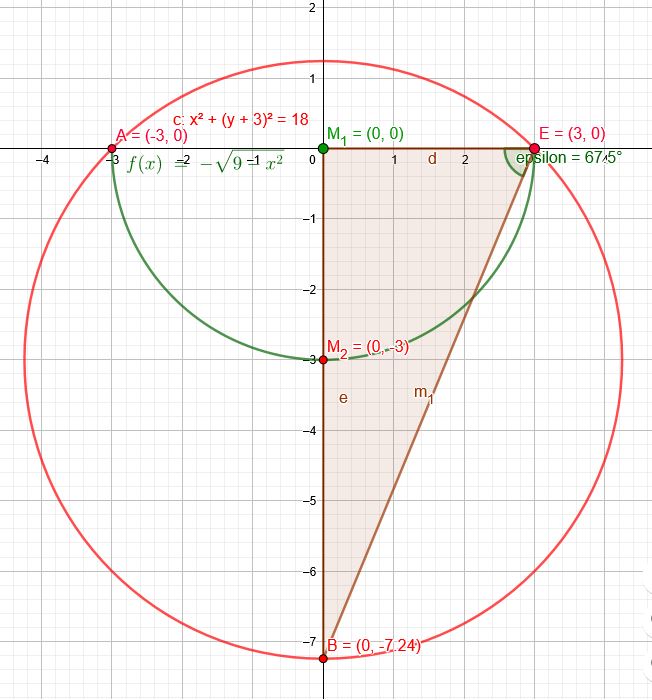
Berechnung des Winkels bei E:
grüner Kreis:
\(f(x)= -\sqrt{9-x^2} \)
Dieser Halbkreis hat die Nullstellen bei \(x_1=-3\) und bei \(x_2=3\)
Schnitt mit der y-Achse:
\(f(0)= -\sqrt{9}=-3 \)
Der rote Kreis hat somit den Mittelpunkt \(M_2(0|-3)\) und geht durch \(A(-3|0)\) und \(E(3|0)\)
c: \(x^2+(y+3)^2=r^2\)
\(E(3|0)\):
\(3^2+(0+3)^2=r^2\)
\(r^2=18\)
c:\(x^2+(y+3)^2=18\)
Berechnung des Schnittpunktes bei B:\((0|?)\)
\((y+3)^2=18 |\pm\sqrt{~~}\)
1.)
\(y+3=\sqrt{18}=3\cdot\sqrt{2}\)
\(y_1=-3+3\cdot\sqrt{2}\) entfällt als Lösung
2.)
\(y+3=-\sqrt{18}=-3\cdot\sqrt{2}\)
\(y_2=-3-3\cdot\sqrt{2}\)
B:\((0|-3-3\cdot\sqrt{2})\) → B:\((0|-7,24\)
Berechnung von \(ε\):
\(tan(ε)=-\frac{7,24}{3}\)
\(tan^{-1}(-\frac{7,24}{3})=-67,49° \)
\(ε=67,49°\)