Bildern komplexer Mengen Funktionen zuordnen. Konforme Abbildungen?

Question

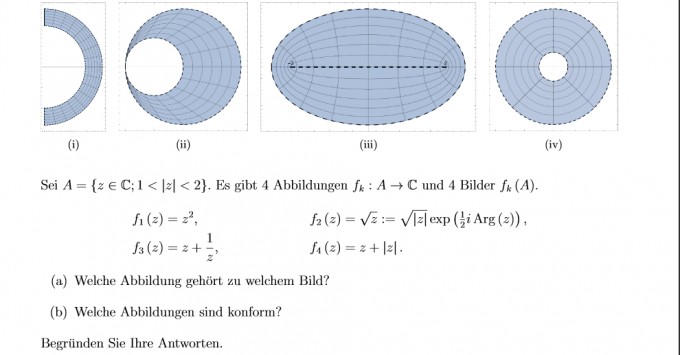
Ich habe Probleme beim zuordnen. Vorallem, weil die Menge aus der abgebildet wird eingeschränkt ist. Außerdem ist auch kein Koordinatensystem eingezeichnet. Das macht das Einsetzen von Punkten schwer.

Ich vermute, dass f1 von (iv.) beschrieben wird. Das "Loch" in der Menge sind Quadrate von |z|<1.

f2 könnte (i) sein, da Arg(z) im Intervall [0,2PI] liegt und e^{1/2i*Arg(z)} damit einen Halbkreis bildet.(eventuell gedreht ist die Abbildung gedreht? Wobei  mich hier die durchgezogene Linie oben an der Abbildung irritiert)

Kann mir da jemand vielleicht helfen?

b) Ich würde sagen, dass nur (iv) konform ist, da das Bild der Ursprungsmenge ähnelt.(Winkel bleiben erhalten...)

Comments

Beim Quadrieren bleiben eigentlich die Winkel nicht gleich.

Die Argumente der Zahlen verdoppeln sich ja.

" f1 von (iv.) " einverstanden, aber das skizzierte Bild wird eigentlich 2 mal "abgefahren". 

Das heisst dann für mich ausserdem, dass (i) zu f2, d.h. der Wurzel gehört. 

Wie ist "konform" definiert? 

---

Eine Abbildung heißt konform, wenn glatte Kurven in glatte Kurven überführt werden und diese Abbildung winkel-und orientierungsgetreu ist.

---

Danke. Das mit den Winkeln würde ich entschieden bestreiten, wenn z=0 im fraglichen Gebiet wäre. Ob das auf dem Ring um z=0 so sein kann, kann ich leider nicht beurteilen. Lokal vielleicht, aber ich zweifle schon etwas.

Ist nicht g(z)= 1/z winkeltreu?

Dann sollte es auch mit f(z) = z + 1/z eigentlich auch so sein.

Answer 1

wenn |z| zwischen 1 und 2 liegt, dann liegt |z^2| zwischen 1 und 4 und weil alle winkel von 0 bis 2pi bei z vorkommen, tun sie dies bei z^2 auch.Also ist f1 passend zu (iv).

bei z + |z| findet ja nur eine Ausdehnung in Richtung der Re-Achse statt. Dazu passt die Ellipse, und
die bei A fehlenden ( Betrag < 1 ) werden durch sowas wie  -1 + |-1|  = 0  etc erreicht.
Also f4 zu ( iii)

bei f2 liegen die Beträge der Ergebnisse zwischen 1 und wurzel(2), das kann nur (i) sein.

und das andere passt auch zu (ii)

Comments

Alles klar, danke :)