Was bedeutet eigentlich dx?

Question

dx → Differenzierung nach x bzw. ableiten nach x ??
dt →Differenzierung nach t bzw. ableiten nach t ??? ( kann man auch: ableiten über "t" sagen?)

Ich übe gerade das Substitutionsverfahren beim integrieren und dann kam die folgende Aufgabe:

 3 =∫ dx / (x* ln (x) )           ich würde jetzt u = ln (x) substituieren → 1/x = du / dx ⇔ dx /x = du ⇔ d = du ???

Mir ist aufgefallen, dass ich nicht wirklich verstanden habe, was eigentlich dx, du, dt bedeutet??

Answer 1

In deiner Frage sind eine Menge von Fragen angeführt.

Zuerst die korrekte Substitution

Dann ist die Aussage

 3 =∫ dx / (x* ln (x) ) 

nicht  lösbar. Es fehlen die Integrationsgrenzen.

Bei der Integralrechnung wird die Fläche unterhalb der Kurve in Streifen
aufgeteilt. Streifenbreite Δ x., f ( x ) ist der Funktionswert an der Stelle x
und entspricht der Höhe des Streifens.
Der Flächeninhalt ergibt sich zu
f1 +  Δ x + f2 * Δ x + f3 * Δ x .....
( f1 + f2 + f3 ... ) * Δ x
∑ f ( x ) * Δ x

Wird die Streifenbreite nun unendlich klein schreibt man

∫ f ( x ) dx

Soweit  der Crashkurs zur Integralrechnung.

Wenn du übst und rechnest kannst du dich steigern.
Aber auch nicht mit dem Kopf durch die Wand wollen.

Comments

Mir ist aufgefallen, dass ich nicht wirklich verstanden habe,
was eigentlich dx, du, dt bedeutet??

Ich habe mir selbst die Substitution nochmals klargemacht
und möchte diese anhand der Frage erläutern.

Wir vergessen die Ausgangsfunktion zunächst und betrachten
nur die Funktion u ( x ) = ln ( x ).
Die erste Skizze zeigt dir symbolisch ( sie entspricht nicht ln ( x ) )
eine Funktion u ( x ). Die Steigung u ´( x ) = 1 / x.

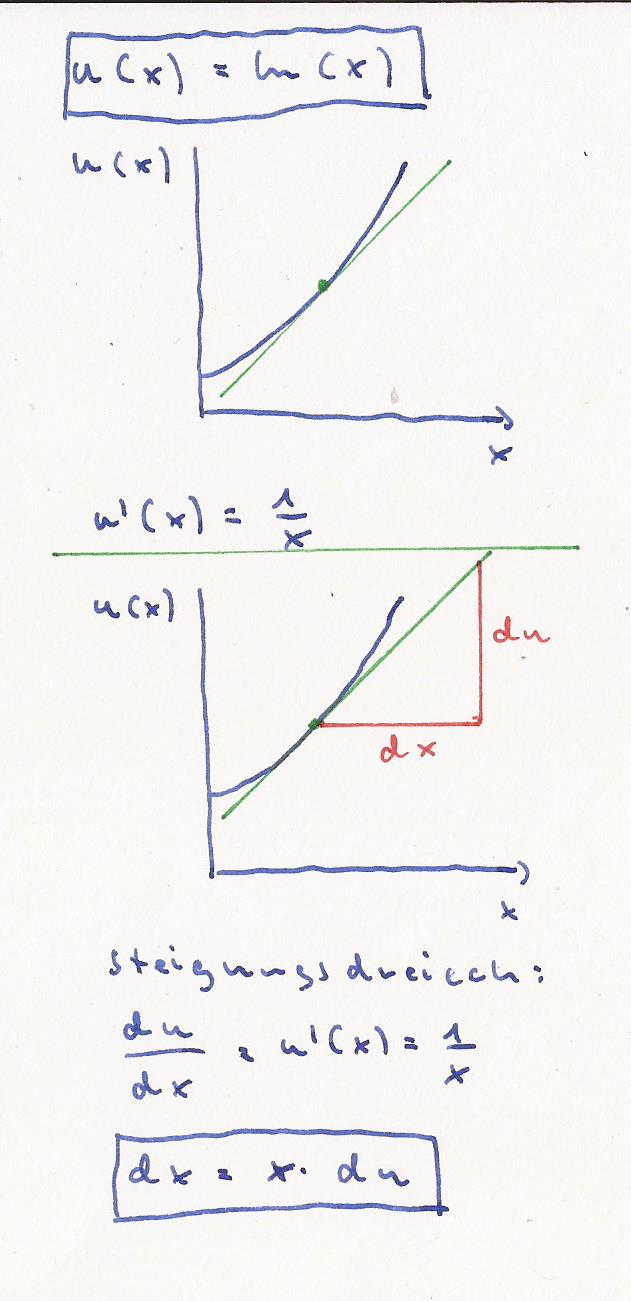In der 2.Skizze habe ich ein Steigungsdreieck, normalerweise Δ u / Δ x, hier
bereits du /  dx eingezeichnet. Für die Steigung gilt

u ´( x ) = 1 / x  = du / dx und nach dx umgestellt :
dx = x * du

Und jetzt zurück zur Ausgangsfunktion. Es wird ersetzt
ln ( x ) durch u
dx durch x * du

∫ 1 / (x* ln (x) )  dx   
∫ 1 / (x* u ) * x du  

Es wurde nicht alles x ersetzt da es sich einmal wegkürzt.
( Dies kommt eher selten vor ). Es bleibt

∫ 1 /  u  du  

mit dem wie in der Antwort beschrieben weiter verfahren wird.