Dazu benötigt man die Bernoulli-Formel:
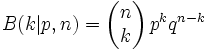
n ist die Anzahl der Versuche (hier 10), k die Anzahl der Treffer, p die Treffer-Wahrscheinlichkeit und q die "Nicht-Treffer"-Wahrscheinlichkeit, also 1 - p.
Daher:
A) P (X = 4) = (10 über 4) * (1/4)4 * (3/4)6 ≈ 14,6%
B) P (X = 0) = (10 über 0) * (1/4)0 * (3/4)10 ≈ 5,63%
C) P (X ≤ 2) = P (X = 0) + P (X = 1) + P (X = 2) = (10 über 0) * (1/4)0 * (3/4)10 + (10 über 1) * (1/4)1 * (3/4)9 + (10 über 2) * (1/4)2 * (3/4)8 ≈ 52,56%
Falls du Bernoulli bisher nicht kanntest: Um einen Bernoulli-Versuch handelt es sich immer, wenn ein bestimmter Versuch mit nur 2 möglichen Ergebnissen quasi mehrmals wiederholt wird und dabei immer die gleiche Wahrscheinlichkeit beibehält. Dann lässt sich immer die Bernoulli-Formel darauf anwenden. :)