V(t)= 50·sin(pi/6·t) + 100
V'(t) = 25·pi·cos(pi/6·t)/3
1. Zum Zeitpunkt t=0 beginnt die Flut. Zeigen Sie dass in der Zeitspanne von 16:00 Uhr bis 4:00 Uhr eine Periode von Ebbe und Flut liegt.
In dem sin steht in der Funktion pi/6. Das bedeutet pi/halbe periode. Die halbe Periode sind also 6 Stunden. Damit sind 12 Stunden eine Periode.
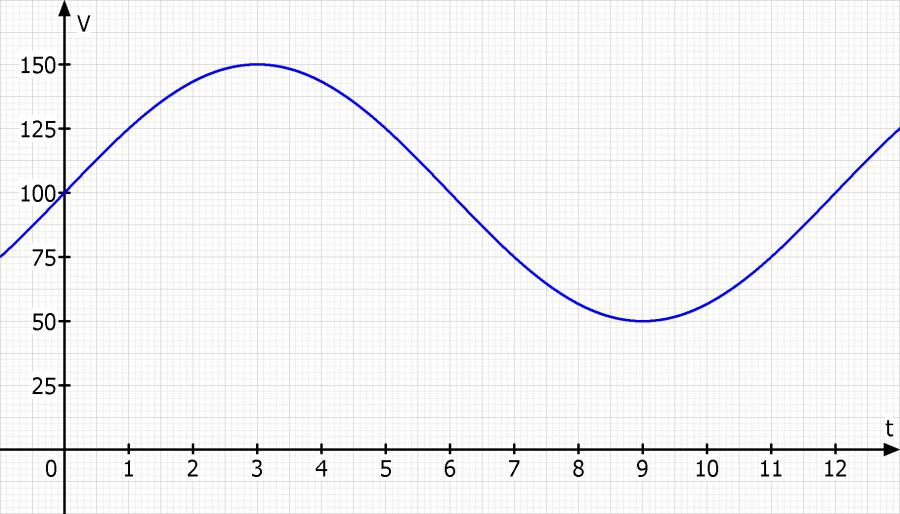
2. Skizzieren Sie den Graf der Funktion V(t) für die erste Periode und interpretieren Sie diesen im Sachzusammenhang. (Maßstab: 1c,=25VE, 1cm=1h)
3.Bestimmen Sie das maximale im Rückhaltebecken befindliche Wasservolumen.
sin() wird maximal 1. Damit ist das maximale Wasservolumen
50*1 + 100 = 150 VE
4.Ermitteln Sie um Welche Uhrzeit während der Zeitspanne von 17 Uhr bis 3 Uhr die Generatorturbinen keine elektrische Energie erzeugen.
Extremstellen hat die Funktion an den Stellen 3 + n*6.
D.h. die erste Extremstelle haben wir bei 19 Uhr und die nächste um 1 Uhr.
5.Die Werte der Ableitungtsfunktion V'(t) geben an:
-das maximale Wasservolumen im Rückhaltebecken (Richtig/Falsch)
Falsch
-das Wasservolumen im Rückhaltebecken zu einer bestimmten Zeit (Richtig/Falsch)
Falsch
-das Wasservolumen welches je Stunde dem Rückhaltebecken zu- bzw. abfließt (Richtig/Falsch)
Richtig. Eigentlich die Momentane Änderungsrate des Zu- und Abflussen.
-die zum Füllen des Rückhaltebeckens benötigte Zeit (Richtig/Falsch)
Falsch
6.Zeigen Sie wie man das mittlere, während einer Periode von Ebbe und Flut im Rückhaltebecken befindliche Wasservolumen bestimmt.
V(t) = 50·sin(pi/6·t) + 100
Stammfunktion
F(t) = 100·t - 300/pi·cos(pi/6·t)
(F(12) - F(0)) / 12 = ((1200 - 300/pi) - (- 300/pi))/12 = 100
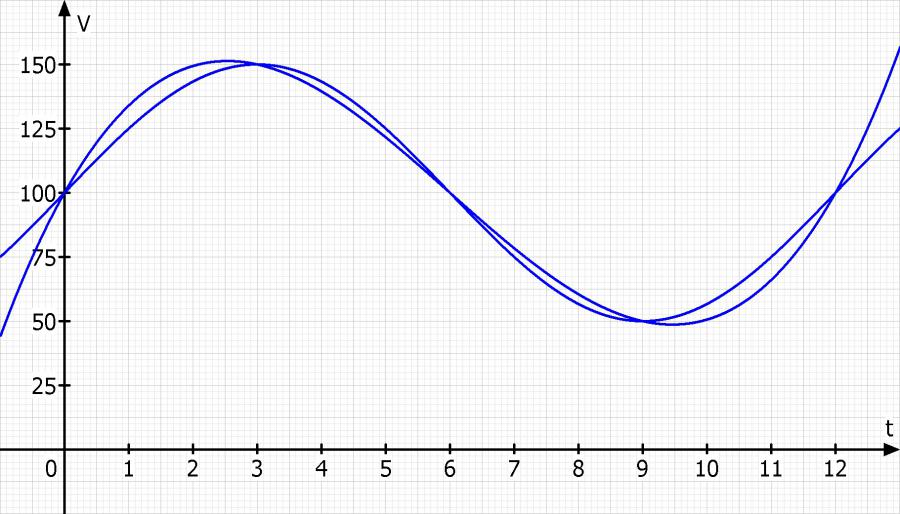
7. Für die Dauer der ersten Periode soll die Funktion V(t) durch eine ganzrationale Funktion geeigneten Grades ersetzt werde. Ermitteln Sie deren Funktionsgleichung f(t).
Das einfachste wär durch eine Funktion 3. Grades
p(t) = a·x·(x - 6)·(x - 12) + 100
p(3) = 150
a·3·(3 - 6)·(3 - 12) + 100 = 150
a = 50/81
p(t) = 50/81·t·(t - 6)·(t - 12) + 100
Ich zeichne sie mal zum Vergleich auch ins Koordinatensystem