Stellen sie den mittleren Jahresgang der Maximaltemperatur als eine veränderte Sinuskurve dar!

Question

Also wie man eine Sinuskurve zeichnet weiß ich, aber ich verstehe nicht, wie ich anhand dieses Diagrammes an Werte für die Sinuskurve kommen soll.

Comments

!! Jetzt habe ich endlich einen richtigen Ansatzpunkt!! Nochmals danke!!!

Answer 1

Stell dir die normale Sinuskurve vor.
Die x-Achse ist in Bogenmass angegeben.

im ersten Schritt müssen wird die Tagangabe in Bogenmass
umwandeln.
Bei der Tagangabe fangen wir
1.1. = Tag 0
1.7. = Tag 180

Nun ist es aus der Grafik ersichtlich das
1.1. = Tag 0 = Tiefpunkt
1.7. = Tag 180 = Hochpunkt

Bei der sinus-Funktion ist
-PI/2 = Tiefpunkt
PI / 2 = Hochpunkt

Für eine Umrechnung sind die Punkte
( 0  | -PI/2 ) ( 180 | PI/2 )
Linieare Funktion
m = ( y1 - y2 ) / ( x1 - x2 ) = ( Pi/2 - (-PI/2) ) / ( 180 - 0 ) = PI / 180
PI/2 = PI/180 * 180 + b
b = - PI /2

Die Funktion lautet
f ( x ) = x * PI / 180  - PI / 2

Diese kann ich direkt  in die max - Funktion einbauen
max ( x ) = sin ( x * PI / 180 - PI/2 )

Tiefpunkt bei 0 Tage : 19 °
Hochpunkt bei 180 Tage : 35 °
Mittlere Temperatur : ( 19 + 35 ) / 2 = 27 °
Amplitude ± 8 °
Die sin Funktion hat eine Amplitude von ± 1
Um auf eine Amplitude von 8 zu kommen muß ich
mit 8 multipliziern
max ( x ) = sin ( x * PI / 180 - PI/2 ) * 8

Jetzt muß ich noch diese Funktion in  Richtung y-Achse nach
oben verschieben um die Mittellinie von 0 ° auf 27 ° anzuheben.

max ( x ) = sin ( x * PI / 180 - PI/2 ) * 8 + 27

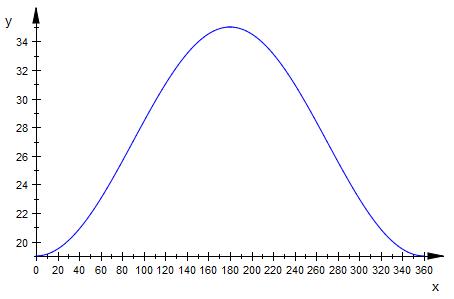
Plotte dir am besten jeden Schritt einmal aus.

Bin bei Bedarf gern weiter behilflich.

Answer 2

Ich denke es ist ein Funktionsterm gefragt. Ich würde das wie folgt modellieren

Mittlere Maximaltemperatur: (19 + 36)/2 = 27.5 Grad
Amplitude: 27.5 - 19 = 8.5 Grad
Periodenlänge: 12 Monate

y = 8.5·SIN(2·pi/12·(x - 4)) + 27.5

Hier liegt das Minimum genau im Januar und das Maximum im Juli. Da es grafisch etwas weiter rechts ist könnte man hier also auch in der Gleichung statt 4 einfach 4.1 schreiben. Der einfachheit halber habe ich oben aber nur die 4 genommen.

Answer 3

f(x)= a+b*sin(c+dx)

abgelesene Werte (ca.) Tiefpu(2|14) Hochpu(8|28)

Also a= (28+14)/2 = 21  und b=(28-14)/2 = 7

d ist zuständig für die Periodenlänge

d=1 führt zu Periode 2pi

du brauchst Periode 12 (1Jahr) also

d= 2pi/12 = 0,523

und der 1. Tiefpunkt soll bei 2 liegen, "normal (also für c=0)" ist 3pi/2

also   c+d*2=3pi/2

also c=3,666. Sieht dann so aus

~plot~21+7*sin(0,523x+3,666); [[0|13|12|30]]~plot~