Inverse Matrix? Determinante beweisen...

Question

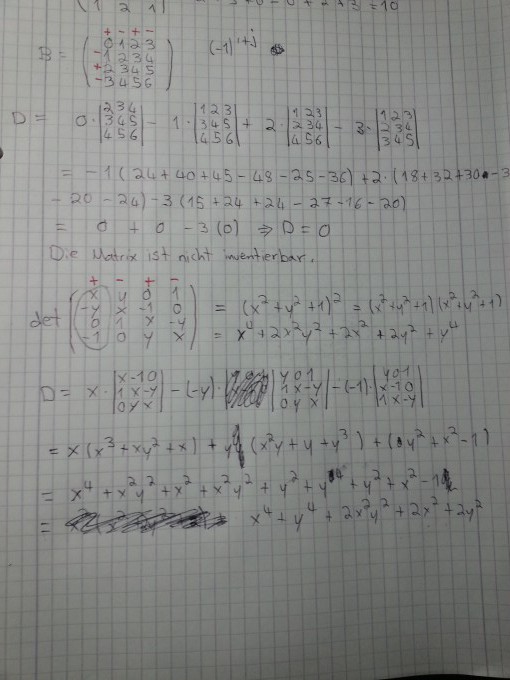
Bei der ersten Aufgabe soll ich untersuchen, ob die Matrix B inventierbar ist. Ist das Ergebnis korrekt, gibt es einen schnelleren Weg?

Nach dem Satz "die Matrix ist nicht inventierbar", kommt folgende Aufgabe: Man zeige mit Hilfe des Laplaceschen Entwicklungssatzes, dass für gilt: 

Ich bin eigentlich fertig nur die +1 fehlt mir, nach meiner Rechnung ergab sich -1 (siehe Arbeitsblatt unten)

Die roten Vorzeichen sind eine Orientierung für mich, einfach ignorieren ;)

Comments

Die Summe aus dem zweiten und vierten Spaltenvektor von  B  ergibt das Doppelte des dritten. Damit sind die Spaltenvektoren linear abhängig, d.h. die Matrix ist singulär.

Answer 1

Die 3. Determinante in deiner Entwicklung hat

den Wert x² + y² + 1   ( nicht -1)

z.B. mit Regel von Sarrus oder so.