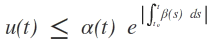Zeigen Sie die Aussage des Gronwall-Lemmas für t ≤ t0
Gronwall-Lemma:
Sei I⊆ℝ ein bel. Intervall mit t0∈I und seien α,β,u:I→ℝ0+ stetige Funktionen.
Ferner erfülle u für alle t∈I die implizierte Abschätzung
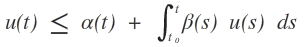
Dann erfüllt u für alle t∈I die explizierte Abschätzung
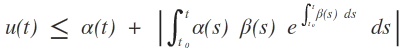
Falls eine monoton steigende Funktion a≥0 existiert, so dass die Form α(t) = a(|t-t0|) besitzt, so vereinfacht sich die obige Abschätzung zu