Die Wahrscheinlichkeit
P1 bei einem Wurf genau
n Augen zu würfeln, ist:
$$ { P }_{ 1 }=\frac { 1 }{ 6 } $$
Die Wahrscheinlichkeit
P2(
n) bei einem Wurf weniger als
n Augen zu würfeln, ist:
$$ { P }_{ 2 }\left( n \right) =\frac { \left( n-1 \right) }{ 6 } $$
Wenn Spieler 1 die Augenzahl n vorlegt, dann gewinnt er, wenn Spieler 2 zweimal eine gleiche oder kleinere Augenzahl würfelt. Die Wahrscheinlichkeit P3(n) dafür beträgt:
$$ { P }_{ 3 }\left( n \right) ={ P }_{ 2 }\left( n+1 \right) \cdot { P }_{ 2 }\left( n+1 \right) =\frac { { n }^{ 2 } }{ 36 } $$
Als nächstes geht es um die Wahrscheinlichkeit P4(n; k) dafür, dass Spieler 1 mit der Strategie Sk die Augenzahl n vorlegt.
Wenn n < k ist, dann muss Spieler 1 zweimal gewürfelt haben, d.h. auch für den ersten Wurf muss n < k gelten.
Wenn n ≥ k ist, dann kann es sein, dass die Augenzahl n beim ersten Wurf erreicht wurde oder beim zweiten Wurf, wenn der erste Wurf kleiner als k war.
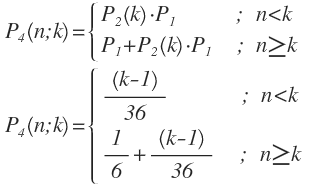
Die gesuchte Wahrscheinlichkeit P(k) dafür, dass Spieler 1 mit der Strategie Sk gewinnt, beträgt:
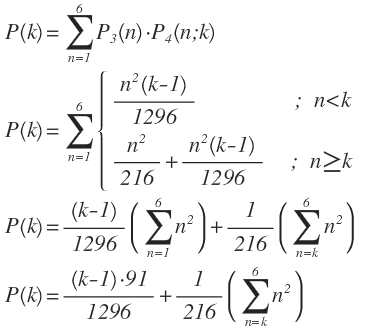
Damit erhält man folgende Gewinnwahrscheinlichkeiten in Abhängigkeit von k:
k
|
P(k)
|
1
|
0,421
|
2
|
0,487
|
3
|
0,539
|
4
|
0,567
|
5
|
0,563
|
6
|
0,518
|