Ist U eine Gruppe bezüglich der Multiplikation von Matrizen?

Question

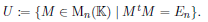
U sei eine Teilmenge von M_n(K).

Ich soll zeigen, ob U ein Unterraum von M_n(K) ist oder nicht. Da bin ich auf den Schluss gekommen nein durch das Beispiel 5*[0,1;1,0]

Und dann soll ich noch zeigen, ob U eine Gruppe bezüglich der Matrizenmultiplikation ist. Dazu Muss die Multiplikation ja assoziativ sein, es braucht ein Einselement und es braucht ein Inverses.

Dass jedes Element in U ein Inverses hat ist klar den immer die Transponierte Matrix ist ja die Inverse.

Ich muss also noch zeigen, dass [1,0;0,1] ein Element von U ist und dass es Assoziativ ist.  Das das Einselement drin ist zeige ich indem ich einfach die Transponierte Matrix und die Einheitsmatrix multipliziere und dann sehe ich, dass wieder die Einheitsmatrix rauskommt, also ist klar, dass auch das Einselement in U ist. Es bleibt also die assoziativität zu zeigen:

Ich weiss dass die Matrizenmultiplikation assoziativ ist, wie zeige ich aber, dass die Multiplikation von Matrizen überhaupt eine Verknüpfung auf der Menge U definiert?? 

Answer 1

\(U\) ist abgeschlossen bezüglich der Multiplikation, denn für zwei Matrizen \(A,B \in M_n(\mathbb{K})\) gilt:

$$ (A \cdot B)^t = B^t \cdot A^t $$

Gruß