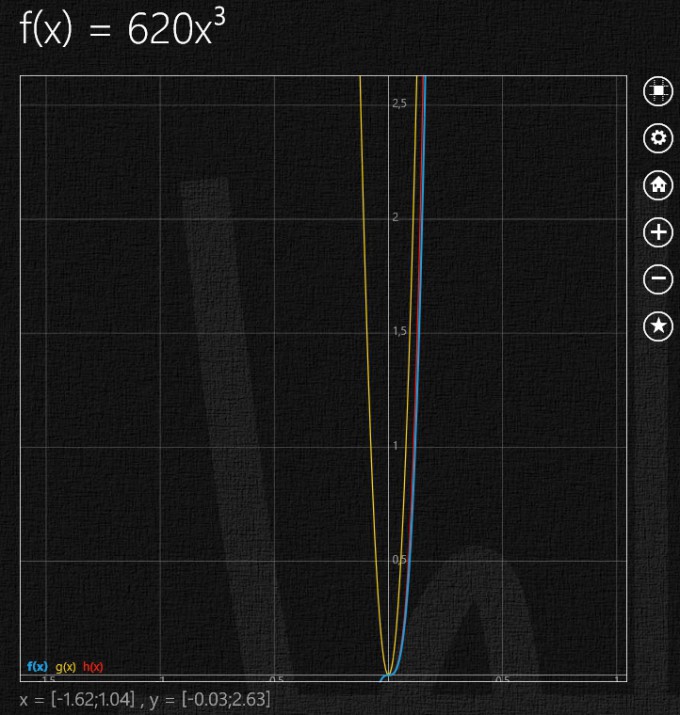
Blaue Funktion (♂): ω=620g/m³·l3
Gelbe Funktion (b): ω=170g/m²·l2
Rote Funktion (♀): ω=744g/m³·l3
Die rote Funktion ist zwischen der blauen und gelben Funktion. Mit welchem Programm kann man die Funktionen doppelt-logarithmisch auftragen? Denn die Funktionen sind nur in normaler Achseneinteilung dargestellt. Eine logarithmische Einteilung ist doch 10, 100, 100 usw., oder?