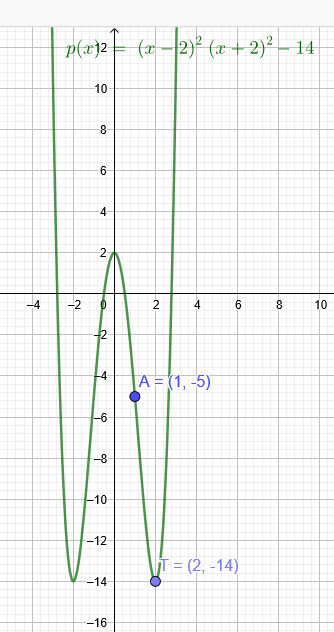
"Bestimmen Sie die Gleichung einer ganzrationalen Funktion vierten Grades, deren Graph symmetrisch zur y-Achse T(2|-14) einen Tiefpunkt hat und durch den Punkt A(1|-5) verläuft."
Ich verschiebe den Graphen von f(x) um 14 Einheiten nach oben:
\(T(2|-14)→T´(2|0)\) doppelte Nullstelle
\(f(x)=a*(x-2)^2*(x+2)^2\) wegen Symmetrie zur y-Achse
\(A(1|-5)→A´(1|9)\)
\(f(1)=a*(1-2)^2*(1+2)^2=9a\)
\(9a=9→a=1\)
\(f(x)=(x-2)^2*(x+2)^2\)
Nun wieder 14 Einheiten nach unten:
\(p(x)=(x-2)^2*(x+2)^2-14\)