Einfacher Beweis mit viel Schreibaufwand, leider verwirrt
ich soll das hier beweisen, also habe ich die einzelnen Ergebnisse ausgerechnet, alles ausgeschrieben, um später zu sehen, dass da das gleiche rauskommt.. Dafür habe mit den Variablen gerechnet..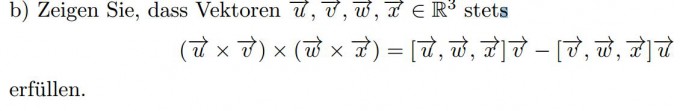
Auch wenn ich vernünftige wenn auch lange Ergebnisse raus habe passt mein
(u X c)x(w X x) Ergebnis nicht mit dem ([u,w,x,]v - [v,w,x,]u)= Vektor Ergebnis zusammen,das müsste ja gleich sein.
(u X c)x(w X x) = Vektor =
=(u3v1-u1v3*w1x2-w2x1-w2x1-u1v2-u2v1*w3x1-w1x3 , u1v1-u2v3*w2x2-w3x1-u2v3-u3v2*w3x1*w1x1-w1x3 , u2v3-u3v2*w3x1-w1x3-u3v1-u3v1*u3v1*u1v3-w3x3-w3x2 )
Das andere ist ja eigentlich nur die Determinante von 3 mal den Vektor v und u, nachdem ch das gemacht habe und die beiden voneinander subtrahieren will, kommt nicht u X c)x(w X x) raus.
Danke