Wie kann ich die Lösungsmenge durch Fallunterscheidung bestimmen?

Question

2 Antworten

Ein anderes Problem?

Johann Ribert · Answer 1 · 2013-05-27T21:12:09+0000

Also ich sach ma es gibt drei Fälle:

1. Fall: x > 3

3(x+2) < 7(3-x); //Vorzeichen kehrt sich um, da 3-x negativ ist

Keine Lösung für x.

2. Fall: -2 < x < 3

x > 1,5; //Vorzeichen bleibt wie es ist, da die Brüche positiv sind

3. Fall: x < -2

x < 1,5; //Vorzeichen kehrt sich um da mit (2+x) multipliziert wird und das negativ ist

lg JR

Gast · Answer 2 · 2013-05-27T21:21:08+0000

Hier sollte man drei Fälle unterscheiden.

(1) x < -2.
Links steht eine positive Zahl und rechts eine negative. Daher gilt die Aussage für alle x.

(2) -2 < x < 3.
Auf beiden Seiten steht eine positive Zahl, d.h. es gilt
3/(3 - x) < 7/(2 + x) ⇔ 3(2 + x) < 7(3 - x) ⇔ x > 1.5.

(3) x > 3.
Links steht eine negative Zahl und rechts eine positive. Daher gilt die Aussage für kein x.

Lösungsmenge ist demzufolge L = { x ∈ ℝ | x < -2 ∨ 1.5 < x < 3 }.
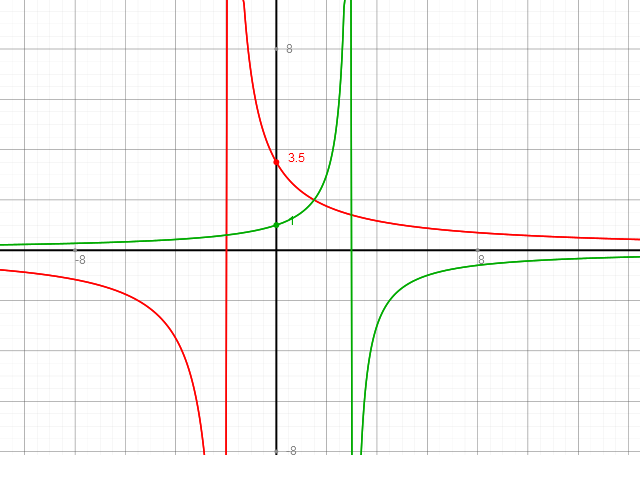
Vgl. Skizze. Schaubilder von 3/(3 - x) und 7/(2 + x).