Question

Bestimmen Sie die reellen Zahlen für a, b und c im Term f(x)=(ax²+bx+c)e^-x  der Funktion f so, dass G(f) an der Stelle 2 einen Hochpunkt hat und die x-Achse im Koordinatenursprung berührt.

Comments

Vom Duplikat:

Titel: Anwendung der Differentialrechnung

Stichworte: differentialrechnung,funktion

Bestimmen Sie die reellen Zahlen für a, b und c im Term f(x)=(ax²+bx+c)e^-x  der Funktion f so, dass G(f) an der Stelle 2 einen Hochpunkt hat und die x-Achse im Koordinatenursprung berührt.

Answer 1

 f(x) = (ax² + bx + c) • e^-x 

Produktregel:

f '(x) = - e^-x ·(a·x² - 2a·x - b + c)

Bedingungen:

f(0) = 0    →   c = 0 

f '(0) = 0   →  b = 0

also:

 f(x) = a·x² · e^-x

f '(x) = - e^-x ·(ax² - 2ax )

f '(2) = 0   ⇔  - e^-x · (4a - 4a) = 0  → a beliebig 

f '' (x) = ax ·e^-x ·(2-x)  muss wegen des Hochpunkts bei  x = -2 dort eine Vorzeichenwechsel von + → - haben, also muss a positiv sein.

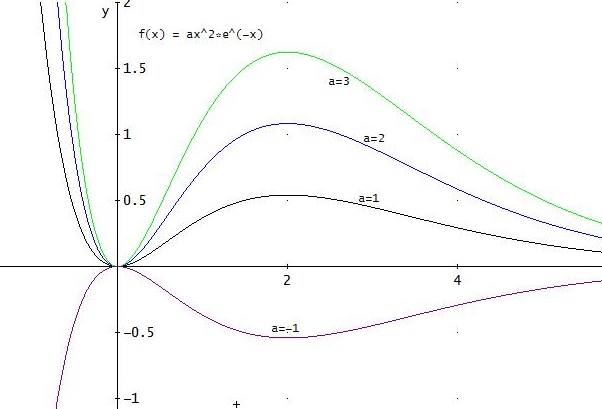
→  f(x) = a·x² · e^-x  mit a > 0.

Zur Verdeutlichung:

Gruß Wolfgang