Kurvendiskussion mit drei Funktionen

Question

ich bin hoffnungslos überfordert. Vielleicht könnt Ihr hier etwas Starthilfe geben. Die Aufgabestellung habe ich als Photo angehängt. Ich kann prinzipiell ableiten sowie Extrema und Wendepunkte/Nullstellen bestimmen. Aber bei dieser Aufgabe weiß ich an einigen Punkten nicht weiter.

a) Bei dieser Aufgabe muss man wahrscheinlich von Nullstellen oder sonstigen Parametern auf den Graphen schließen? Ich kann mir nur vorstellen das f3 blau ist, da es die einzige "x hoch3" ist, und diese einen anderen Verlauf als rot und braun hat.

b)Ich habe alle Funktionen addiert und mit meinen bescheidenen Künsten kommt
2xhoch3 - 10xhoch2 heraus. Richtig soweit, bis auf die Schreibweise?

c)keine idee

d)wahrscheinlich eine Symmetrie?

e)Wendepunkt ausrechnen, dann Tangentengleichung für Wendepunkt aufstellen, dann Tangentengleichung für die Nullstelle aufstellen - und dann was geometrisches um an den Winkel zu kommen? Bis auf das es wahrscheinlich meine Fähigkeiten übersteigt, liege ich tendenziell richtig?

Vielen Dank für alles was Ihr mir bieten könnt

Stevie

Answer 1

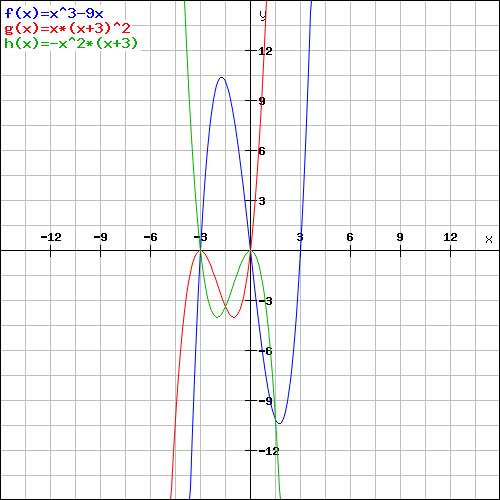
zu a)

f₁(x) = x³ - 9x | Null setzen
ð            x³ - 9x = 0 | x ausklammern

ð            x*(x² - 9) = 0 => x = 0 und (x² - 9) = 0 | 3. Binom => (x+3)*(x-3) = 0

ð            x₂: x+3 = 0 => x₂ = -3 und x₃: x-3 = 0 => x₃ = 3 

Versuche es mit den beiden anderen analog

zu b)

x³ - 9x + x*(x+3)² + (-x²*(x+3)) = 0

x³ - 9x + x*(x² + 6x + 9) + (-x³ – 3x2) = 0

x³ - 9x + x³ + 6x² + 9x -x³ - 3x² = 0

x³ + 3x² | x² ausklammern

x2*(x+3)=0

x₁ = 0

x₂ = -3

Nullstellen berechnen

f’(x) = 3x² + 6x | :3

f’(x) =x² + 2x | p=2; q=0

x₁/₂ = -p/2 +-Wurzel ((p/2)²-0)

x1/₂ = -1 +- 1 => x₁ = 0 und x₂ = -2