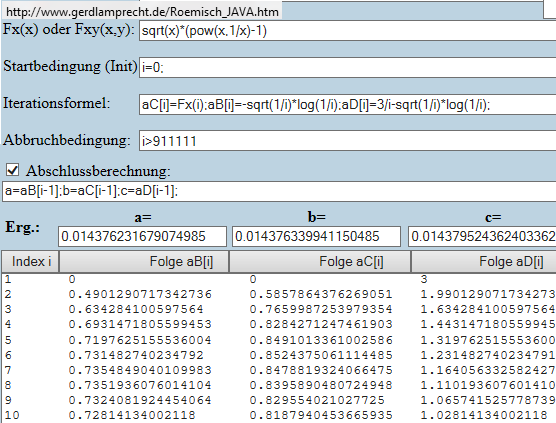
f(x) = sqrt(x)*(x^{1/x}-1) mit sqrt=Wurzel
lim f(x) =0 für x->∞
Beweis:
Mit Hilfe von https://en.wikipedia.org/wiki/Puiseux_series
kann man eine Serienentwicklung (Näherungsformel) aufstellen:
f1(x)=-sqrt(1/x)*log(1/x)
f(x) = f1(x) + Rest(x) mit Rest(x) < 3/x
f2(x) = 3/x-sqrt(1/x)*log(1/x)
für x>6 gilt: alle 3 sind monoton fallend mit:
f1(x) <= f(x) <= f2(x)
lim f1(x), x->∞ =0
lim f2(x), x->∞ =0
Da f(x) immer zwischen beiden liegt, kann der Grenzwert auch nur 0 sein!
Was der Iterationsrechner online beweist { x^y=pow(x,y) }:
http://www.gerdlamprecht.de/Roemisch_JAVA.htm