folgende Aufgabe ist gegeben:

(i)
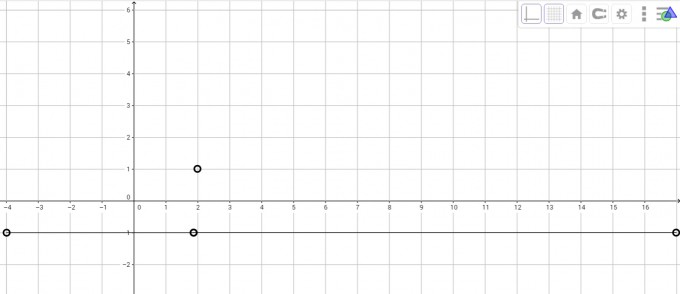
(ii)
f(2)-1=0
f(2)+1=0
(iii)
$$\underset { x\rightarrow { 2 }^{ - } }{ lim } f(x)=-1\\ \underset { x\rightarrow { 2 }^{ + } }{ lim } f(x)=1$$
(iv)
Kein Grenzwert, weil
$$\underset { x\rightarrow { 2 }^{ - } }{ lim } f(x)\neq \underset { x\rightarrow { 2 }^{ + } }{ lim } f(x)$$
(v)
Nicht stetig, da die Funktion f(x) nicht ohne abzusetzen gezeichnet werden kann (nicht definierte Stellen bei x=2 sowohl bei f(x)=1 als auch bei f(x)=-1.
Ich bin mir nicht sicher, ob meine Lösungen korrekt sind.
Beste Grüße,
Asterix