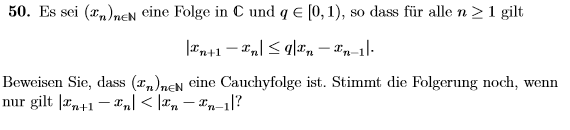Beweis einer Cauchyfolge in C

Question

Hallo ich habe folgende Aufgabenstellung (Bild), bei der ich um Hilfe suche .Für eine CF muss das Cauchy Kriterium erfüllt sein , welches besagt dass:eine Folge in R oder C  konvergiert gegen einen Grenzwert in den reellen bzw. komplexen Zahlen, wenn es zu jedem Epsilon >0 einen Index N gibt, sodass der Abstand zweier beliebiger Folgenglieder ab diesem Index kleiner als Epsilon ist.  Der Abstand von xn+1 zu xn ist dabei ja kleiner als der von xn zu xn-1 . da mit steigenden Index die Abstände der benachbarten Folgenglieder ja kleiner werden , man kompensiert hier ein <= mit einem gewissen faktor q aus [0,1) was heißt das| xn-xn-1 | echt größer sein muss als |xn+1-xn|.Wie zeigt man das jedoch?

Answer 1

Hallo arni,

mit den folgenden zwei Schritten solltest du zum Ziel kommen.

Sei \(D := |x_1-x_0| \). Zeige:

1) \( |x_{n+1}-x_n| \leq q^n D \) für alle \(n \geq 1\).

2)\(|x_m - x_N| \leq q^ND \sum\limits_{k=0}^{m-(N+1)} q^k \) für \(m \geq N \geq 1 \).

Gruß

Comments

Hallo und Vielen Dank das werde ich gleich probieren !

Gruß

---

Den punkt i) Hab ich mit Induktion gemacht.

zu ii) fällt mir ein das die gennante Summe die Form einer geometrischen Reihe hat.Falls q<1 ist (was hier der Fall ist) ist der Limes hiervon 1/(1-q) .Oder anders ausgedrückt , wir haben in der Vo eine Formel dafür gefunden die lautet sn= [1-q^{n+1}]/(1-q) in diesem Fall wäre das sn= [1-q^{m-N+2}]/(1-q)

aber verstehe nicht ganz wie man ii) zeigt.

---

Genau mit der geometrischen Reihe kannst du eine weitere Abschätzung nach oben durchziehen und befindest dich quasi auf der Zielgeraden.

Um ii) zu zeigen verwende i) und die Dreiecksungleichung.

---

Puh diese Abschätzungen sind nicht leicht bzw. rauben mir ein wenig meine Nerven.

Wie geht man hier vor?, Ichs verstehs leider nicht .:(

---

Dazu müsstest du ein wenig spezieller werden wo genau wir beide grade sind ^^.

---

Ok natürlich ^^. Bei ganz  ii) .

---

\(|x_m-x_N| \leq |x_m-x_{m-1}| + |x_{m-1}-x_{m-2}| + \dots + |x_{N+1}-x_N| \).

Edit: Tippfehler.

---

Ok ich Probier mal weiter :)

Warum steht gank links xn und nicht xN?

bzw. wäre auf der rechten seite dann nicht ganz zum schluss xn+1 - xn?

worauf man i) anwenden könnte?

---

Du kannst überall i) anwenden (sollst du sogar), aber das mit dem kleinen \(n\) war ein Tippfehler meinerseits, den ich jetzt behebe :).

---

oh ok :) dann ist die rechte seite doch ≤ (wegen i) ) q^{m-(N+1)}*|xN+1-xN|≤q^{m-(N+1)+N}*D

hmm jz müsste ich irgendwie die Geometrische Reihe Einbauen.

---

Nein, das wäre ja nur einer der Summanden, Du musst für alle Summanden i) benutze, daher kommt auch die Summe in meiner Antwort bei 2) zustande.

---

Asoo dann brauche ich für jeden einzelnen Summanden ein bestimmtes q^k was mit der Summe ausgedrückt wurde .Die die Anzahl der Summanden beschreibt was erechent wurde als Differenz des höchsten Summanden - kleinster Summand. Und darauf noch i ) angwendet ergibt die Aussage dann?

---

Im Grunde ja :).