Wie begründe ich das geometrische Mittel mithilfe des Satzes von Pythagoras?

Question

 

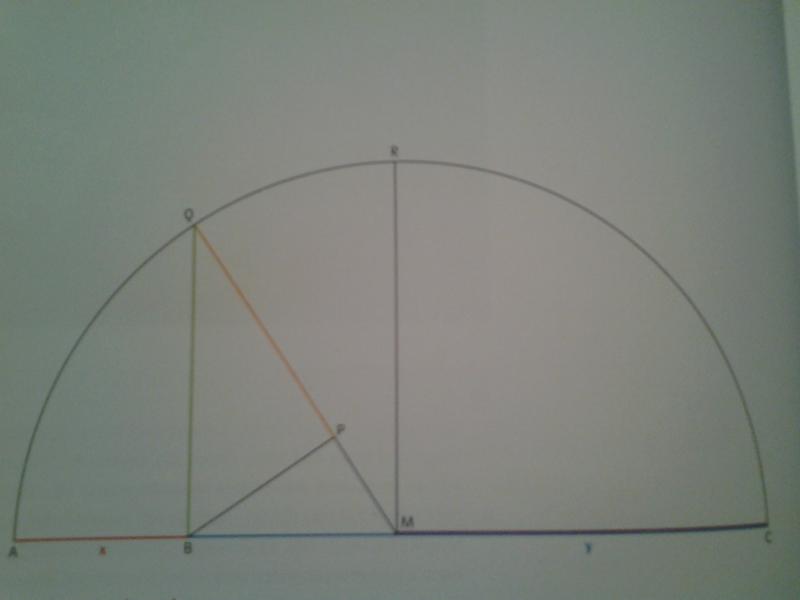
Meine Aufgabe lautet: Die Länge der Strecke BQ (also die grüne Strecke) ist gerade so lang wie die Wurzel aus x mal y.  Das bezeichnet man auch als geometrisches Mittel von x und y. Begründe mithilfe des Satzes von Pythagoras.

(x ist rot, zwischen A und B, und y ist blau, zwischen B und C. Zusammen ergeben sie den ganzen Durchmesser.)

 

Wie mach ich das? Falls es hilft, hier sind meine Messungen von der Skizze:

x = 2,9 cm

y = 9,9 cm

Das geometrische Mittel der beiden, also beide multiplizieren und daraus die Wurzel, beträgt dann genau 5,35817133 cm.

Die Strecke BQ beträgt 5,4 cm, also nach meinen Messungen.

 

Mich irritiert das man beim Satz des Pythagoras ja mit plus rechnet (a² + b² = c²), während man aber beim geometrischen Mittel ja mit mal rechnet (die Wurzel aus x mal y.) Wie soll man denn die beiden vergleichen?

 

Ich hoffe, es ist alles verständlich. Ich brauche die Aufgabe auch ziemlich gelöst.

Comments

Vielleicht kannst du hier umformen: (a² + b² = c²)

a^2 = c^2 - b^2 = (c+b)(c-b)

Kommst du so bereits weiter?

Mathecoach hat die die Skizze in die Form des Höhensatzes gebracht. Und dort den gleich noch mit dem Pythagoras bewiesen.

Answer 1

 

a^2 + b^2 = (x + y)^2

x^2 + h^2 + y^2 + h^2 = x^2 + 2xy + y^2

2h^2 = 2xy

h^2 = xy

h = √(xy)

Answer 2

Für das Dreieck BQM gilt:

(BQ)^2+(MB)^2=(QM)^2

BQ=sqrt((QM)^2-(MB)^2)

QM=(y+x)/2

BM=((y+x)/2-x)

(QM)^2=1/2*(x^2+2xy+y^2)

(MB)^2=1/2(x^2-2xy+y^2)

(QM)^2-(MB)^2=4xy

jetzt hab ich eine 4 zu viel... wo die allerdings herkommt weiss ich nicht... Aber vielleicht finde ja wer den Fehler

Answer 3

Das ist eine Typische Anwendung des Höhensatzes von Euklid --> https://de.wikipedia.org/wiki/H%C3%B6hensatz#H.C3.B6hensatz_des_Euklid

Damit ist es eigentlich bewiesen ;-)

Wenn du noch den Rechenweg haben willst, schau beim Mathecoach, welcher eigentlich den Höhensatz bewiesen hat...

Grüsse
Simon