Wie lang und wie breit muss das Rechteck sein, wenn der Flächeninhalt der Figur maximal sein soll

Question

Funktionenscharen aufgabe

Wie lang und wie breit muss das Rechteck sein, wenn der Flächeninhalt maximal sein soll und der Umfang 100 cm beträgt ? Figur : rechteck mit 2 dreiecken als dach direkt nebeneinander auf der längeren seite des rechtecks

Umfang = 6a +2b

EDIT: "der Figur" in Überschrift ergänzt.

Comments

Vom Duplikat:

Titel: Funktionenscharen aufgabe haus

Stichworte: funktionenschar,funktion,kurvendiskussion

Wie lang und wie breit muss das Rechteck sein, wenn der Flächeninhalt maximal sein soll und der Umfang 100 cm beträgt ? Figur : rechteck mit 2 dreiecken als dach direkt nebeneinander auf der längeren seite des rechtecks

Umfang = 6a +2b

---

Bitte veröffentliche noch ein Bild der Figur.

Offensichtlich besteht der Umfang aus 8 Strecken.

Allerdings kann ich nicht ganz nachvollziehen wie.

Answer 1

Wie lang und wie breit muss das Rechteck sein, wenn der Flächeninhalt maximal sein soll und der Umfang 100 cm beträgt ?

Kann man beantworten: jeweils 25 cm, Quadrat ist Rechteck mit maximaler Fläche bei gegebenem Umfang.

Figur : rechteck mit 2 dreiecken als dach direkt nebeneinander auf der längeren seite des rechtecks

Umfang = 6a +2b

Versteht - meine ich - kein Mensch

----------------------------------------

Viel später :-):

Das Wort "Umfang" war der Knackpunkt für meine obigen Worte!

Unter Einbeziehung von Mathecoachs Anmerkungen im Kommentar denke ich jetzt, dass mit dem "Umfang" (U= 4a+2b=100) die "Gesamtlänge der eingezeichneten Strecken" gemeint ist und es nur so aussehen kann:

(Dreiecke kongruent)

 

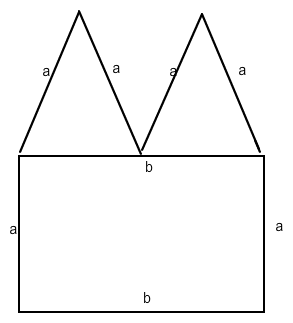
A = A_Rechteck + 2 • A_Dreieck = a • b + 2 • 1/2 • b/2 • √( a² - b²/4 ) = a • b + b/2 • √( a² - b²/4 )

Mit  4a + 2b = 100  → b = 50 - 2a , also:

A = a • (50 - 2a) + (25 - a) • √( a² - (50 - 2a)²/4 )

Jetzt müsste mit A'(a) = 0 die Maximalstelle von A bestimmt werden.

Aber da das Ganze ja nur eine "an Überzeugung grenzende starke Vermutung " ist, überlasse ich den Rest (mit Freude!) meinem Rechner:

A ' (a)  = - (2·(a - 25)·√(2·a - 25) + 15·a - 250) / √(2·a - 25)

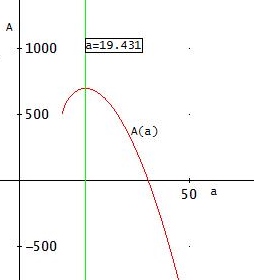
einige Nullstelle von A ' :  a = 725/24 - 325·cos(2·arccot(- 8·√237 / 711) /3) / 12  ≈  19.431

→  ≈  19.431  und  b  ≈ 11,138 

[ allerdings ist b offensichtlich nicht die "längere Seite", aber das soll ja bei Planfiguren vorkommen ]

Gruß Wolfgang

Comments

Naja. Offenbar handelt es sich nicht um ein normales Rechteck. Zumindest das habe ich verstanden. Ich habe das mit den Dreiecken zumindest zum Teil verstanden. Aber ohne eine Bedingung für die Dreiecke zu haben ist es witzlos sich an der Aufgabe zu versuchen. Das kann nur verkehrt werden.

---

Habe auch einige Zeit damit verschwendet, mir das vorzustellen, ist mir aber auch nicht gelungen.

Viel später :-):

Habe die Anmerkungen von MC in meine Überlegungen einbezogen und bin zu einer Überzeugung gekommen, die ich oben in der Antwort ergänzt habe :-)

---

Ok, hier nochmal genaueres zur Aufgabe.

Der Umfang wie ich ihn angegeben habe ist schon richtig: U = 6a+2b ( Ist doch die Nebenbedingung oder? )

Unten auch nochmal eine Skizze zum Verständnis. Wie ihr seht müsst ihr nur die eine Seite ( 2a ) des Rechtecks miteinbeziehen, die andere, also da wo die Dreiecke drauf sind nicht.

Ich kann euch auch noch die Extremalbedingung geben: A = 2ab + 2*√3/4 *a^2 -> a^2/2 * √3 ( gekürzt )

So, in der Schule müssen wir das immer nach dem selben Muster machen : 1. Nebenbedingung 2. Extremalbedingung 3.Zielfunktion.

Die Lösung zur Aufgabe habe ich zwar, verstehe ich allerdings nicht so wirklich deswegen wäre ich froh wenn ihr mir das ganze nochmal erläutern würdet. Und zwar sind die Lösungen einmal a = 9,74 und h = √3/2*a

Grüße

---

Eine Rechteckseite mit  2a  bezeichnen ist natürlich - ohne Bild - eine üble Falle

(genaugenommen "sittenwidrig" :-)).

Ich hatte also recht: versteht kein Mensch. Mathecoach hatte auch recht : Jeder gewaltsame Versuch konnte nur "falsch" werden.

Befasse mich ggf. heute Nacht noch einmal damit.

Wenn die Antwort von MC deine Probleme nicht löst, solltest du in deiner Lösung kommentieren, was du nicht verstehst, und ein Photo einstellen!

Answer 2

U = 6·a + 2·b = 100 --> b = 50 - 3·a

A = 2·√3/4·a + 2·a·b

A = 2·√3/4·a + 2·a·(50 - 3·a) = a·(√3/2 + 100) - 6·a^2

A' = - 12·a + √3/2 + 100 = 0 --> a = √3/24 + 25/3 = 8.405502117

b = 50 - 3·(√3/24 + 25/3) = 25 - √3/8 = 24.78349364