Wie berechnet man einen an einer Ebene reflektierten Strahl?

Question

Hi zusammen, beim Üben von Spiegelungen bin ich auf folgende Aufgabe gestoßen:

Gegeben seien die Ebene E und die Gerade G durch E =(1 ,0, 0)  + span{ (−2, 1, 0 ) , (−1, 0, 1)} , G =(1, 1, 0) + span{(0, 0, −2)}

Ein Lichtstrahl werde vom Punkt (1,1,0)^T entlang von G ausgesendet und an E reflektiert. Berechnen Sie die Parameterdarstellung des reflektierten Strahls.

Ich weiß nicht so recht wie ich diese Aufgabe am besten angehen kann und würde mich über hilfe freuen.

Answer 1

du kannst so vorgehen:

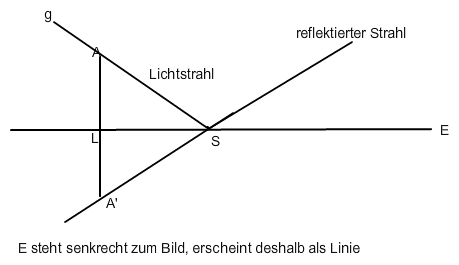
Berechne den Schnittpunkt S von G und E und den Spiegelpunkt A' des Aufpunkts A (Stützvektor ist Ortsvektor von A) von G bzgl.  E.

In der Geraden durch S und A' liegt der reflektierte Strahl.

[ beginnend bei S in Richtung \(\overrightarrow{A'S}\) ]

Gesucht ist also die Halbgerade  \(\vec{x}\) = \(\vec{s}\) + λ •  \(\overrightarrow{A'S}\)  mit  λ ∈ ℝ₀⁺

-----------------------------------

Rechnung: (Alle Spaltenvektoren als Zeile geschrieben)

Das Kreuzprodukt der Richtungsvektoren von E ist ein Normalenvektor von E:

[-2, 1, 0] ⨯ [-1, 0, 1]  =  [1, 2, 1]  =  \(\vec{n}\)

Normalengleichung von E:    [1, 2, 1]  •  \(\vec{x}\) - [1, 2, 1]  • [1, 0, 0] = 0

E = [1, 2, 1]  •  \(\vec{x}\)  - 1 =  0

Für  Schnittpunkt S  von E und G  Geradenterm in E einsetzen und λ bestimmen:

[1, 2, 1]  • (  [1, 1, 0] + λ_s • [0, 0, −2] )   - 1  =   0

Ausmultiplizieren:

3  - 2λ_s - 1 = 0 →  λ_s = 1

λ_s in G:     \(\overrightarrow{OS}\)  =  [1, 1, 0] + 1  • [0, 0, −2]  =  [1, 1, -2]    →  S(1|1|-2)

Spiegelpunkt A' von A( 1, 1, 0) bzgl. E:

Hierzu benötigt man die Lotgerade zu E durch A:    

g_L :   \(\vec{x}\) = [1, 1, 0]  + μ •  [1, 2, 1]    (NV von E = RV der Lotgerade)

L = Lotfußpunkt von g_L in E:   (Schnittpunktberechnung wie oben)

[1, 2, 1]  • (  [1, 1, 0] + μ_L • [1, 2, 1] )   - 1  =   0

3 + 6μ_L - 1 = 0   →  μ_L = -1/3   →  \(\overrightarrow{OL}\) = [2/3, 1/3, -1/3]  →  L (2/3 | 1/3 | -1/3)

\(\overrightarrow{AL}\) = [2/3, 1/3, -1/3] -  [1, 1, 0]  = [ -1/3, -2/3, -1/3]

\(\overrightarrow{OA'}\) =  \(\overrightarrow{OL}\)  + \(\overrightarrow{AL}\) = [ 2/3,1/3, -1/3] + [ -1/3, -2/3, -1/3]  = [1/3, -1/3, -2/3]  

[Edit: Habe hier einen Rechenfehler beseitigt (Dank an MC)]

\(\overrightarrow{A'S}\) = [1, 1, -2]  - [1/3, -1/3 , -2/3]  = [2/3, 4/3, -4/3]

 Halbgerade  \(\vec{x}\) = \(\vec{s}\) + λ •  \(\overrightarrow{A'S}\)  mit  λ ∈ ℝ₀⁺ :

\(\vec{x}\) =  [1, 1, -2] + λ • [ 2/3, 4/3, -4/3 ]     mit  λ ∈ ℝ₀⁺ 

oder mit anderem  λ und vereinfachtem Richtungsvektor (Faktor 2/3 ändert die Richtung nicht):

\(\vec{x}\) =  [1, 1, -2] + λ • [ 1, 2, - 2]     mit  λ ∈ ℝ₀⁺ 

ist die gesuchte Halbgerade, die den Verlauf des reflektierten Strahl angibt.

[ Ich empfehle dir , alles nachzurechnen :-) , denn es ist jetzt 3:58 Uhr!]

Gruß Wolfgang 

Comments

Wäre es vielleicht möglich, dass du es an diesem Beispiel einmal vorrechnest? Das würde mir wirklich weiterhelfen.

---

Es ist immer wieder das Gleiche:

Man beantwortet die Frage

>Ich weiß nicht so recht wie ich diese Aufgabe am besten angehen kann und würde mich über Hilfe freuen.

Dann soll man zwei dafür notwendige aufwändige Grundaufgaben (!) explizit vorrechnen, was dann erfahrungsgemäß weitere Wissenslücken aufdeckt.

Du musst Wissenslücken bei Grundlagen direkt aufarbeiten und nicht erst, wenn Letztere bei komplexeren Aufgaben benötigt werden!

[ Schnittpunkt Gerade/Ebene , Spiegelpunkt von P bzgl. Ebene , so etwas ist in deinem Mathematikbuch mit Sicherheit an Beispielen erklärt! ]

Das ist mit dem Formeleditor ziemlich viel Tipparbeit.

Wenn sich bis dahin sonst niemand findet, mache ich es vielleicht heute seeehr spät (also eigentlich morgen).

Vorher müsste ich aber wissen, ob du mit den Begriffen Normalenvektor und Normalengleichung einer Ebene etwas anfangen kannst?

---

Ja das kann ich und tut mir leid, dass ich dir so viel Mühe mache. Ich werde mich ab jetzt bemühen, meine Wissenslücken früher zu füllen.

Answer 2

Ein Lichtstrahl werde vom Punkt P(1, 1, 0) entlang von g ausgesendet und an E reflektiert. Berechnen Sie die Parameterdarstellung des reflektierten Strahls.

E: X = [1, 0, 0] + r·[-2, 1, 0] + s·[-1, 0, 1]

g: X = [1, 1, 0] + t·[0, 0, -2]

Ebene in Koordinatenform bringen

N = [-2, 1, 0] ⨯ [-1, 0, 1] = [1, 2, 1]

E: X·[1, 2, 1] = [1, 0, 0]·[1, 2, 1] --> x + 2·y + z = 1

Gerade in Ebene einsetzen um Schnittpunkt zu bestimmen

(1) + 2·(1) + (-2·t) = 1 --> t = 1

S = [1, 1, 0] + 1·[0, 0, -2] = [1, 1, -2]

Richtungsvektor an Ebene spiegeln

[0, 0, -2] + r·[1, 2, 1]

(r) + 2·(2·r) + (r - 2) = 0 --> r = 1/3

[0, 0, -2] + 2/3·[1, 2, 1] = [2/3, 4/3, - 4/3] = 2/3·[1, 2, -2]

Reflektierter Strahl

h: X = [1, 1, -2] + r·[-1, -2, 2]

Comments

@Mathecoach:

Habe - dank deines abweichenden Ergebnisses :-) - einen Rechenfehler korrigiert und für den reflektierten Strahl die gleiche "Trägergerade" wie du.

Da der reflektierten Strahl längs einer Halbgeraden verläuft, ist der "orientierte" Richtungsvektor (oder die eingeschränkte Menge von r [ bei dir r∈ℝ₀^- ?] ) wichtig.

Deshalb verstehe ich nicht, warum du den gespiegelten Richtungsvektor mit  -1 multipliziert als Richtungsvektor des Strahls angibst, obwohl dieser - zumindest nach meinem Ergebnis - in die Gegenrichtung des Strahls verläuft?

---

Ja. Das war ein Denkfehler von mir. Wenn ich den Richtunsvektor spiegel befindet er sich zwar an der Falschen Seine der Ebene hat aber ja schon die richtige Richtung. Ich verbesser das.